Inhaltsverzeichnis
Punkte auf elliptischen Kurven
Punktaddition
Wiederhole die Addition von Punkten (Vektorrechnung 5. Klasse)!
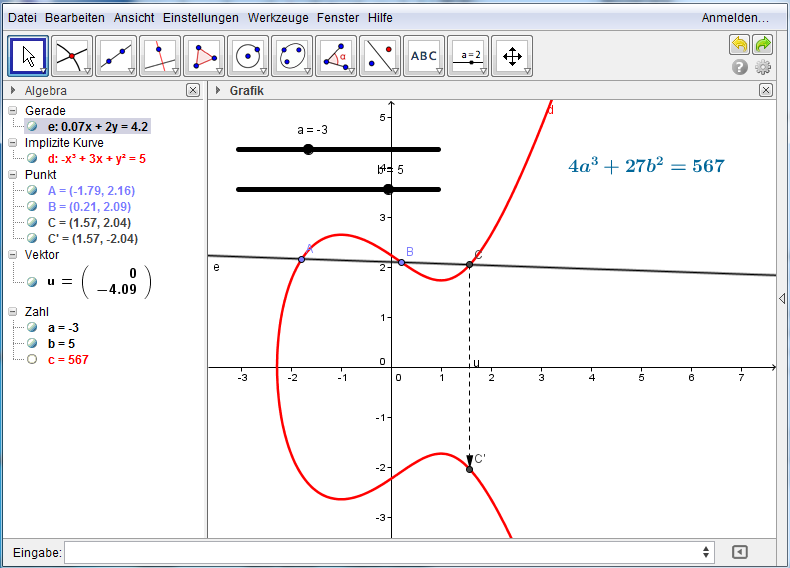
Punkte auf Elliptischen Kurven haben bemerkenswerte Eigenschaften. Für zwei Punkte lässt sich eine Punktaddition geometrisch wie folgt definieren:
Die Addition der beiden Punkte A und B erfolgt dadurch, dass der Schnittpunkt C der Gerade durch A und B mit der elliptischen Kurve an der x-Achse gespiegelt wird: A + B = C'
Aufgaben:
- Begründe, dass die Punktaddition auf elliptischen Kurven das Kommutativgesetz (A + B = B + A) erfüllt!
- Begründe, dass die Punktaddition auf elliptischen Kurven das Assoziativgesetz (A + (B + C) = (A + B) + C) erfüllt!
- Für eine Tangente an die Kurve ohne einen Schnittpunkt mit der Kurve wird
angenommen. Überlege, dass A +
= A gilt!
- Die Punkte A und -A unterscheiden sich durch das Vorzeichen der zweiten Koordinate. Überlege, warum A + (-A) =
gilt („A und -A sind zueinander invers)!
Zahl mal Punkt
Die Multiplikation eines Punktes mit einer Zahl wird über die fortgesetzte Addition festgelegt:
(k Summanden)
Aber wie addieren wir den Punkt „mit sich selbst“???
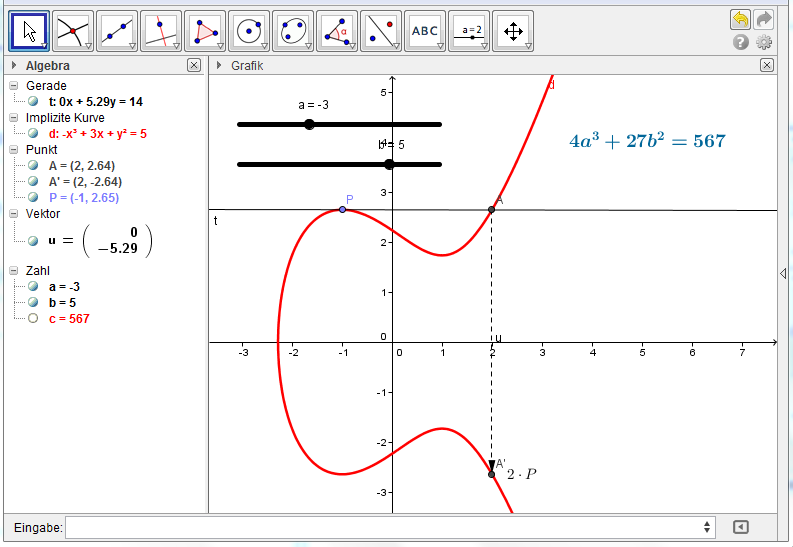
Wir überlegen: Die Addition zweier (getrennter) Punkte A und B führt zu einer Sekante der elliptischen Kurve; rücken diese beiden Punkte immer näher zusammen, so entsteht eine Tangente.
Wir legen also die Tangente an die elliptische Kurve in und schneiden diese mit der Kurve. Der an der x-Achse gespiegelte Punkt ist
:
Algebraische Definitionen...
Bei der Addition der beiden Punkte und
gilt für den Summenpunkt
:
(
) !!!)
Aufgaben
- Überprüfe die obigen Rechengesetze anhand der Definition für die Punktaddition!
- Überlege, dass
bedeutet, dass die Punkte A und B entweder identisch oder an der x-Achse gespiegelt sind. Was bedeutet dies geometrisch?
Zurück zu Elliptische Kurven