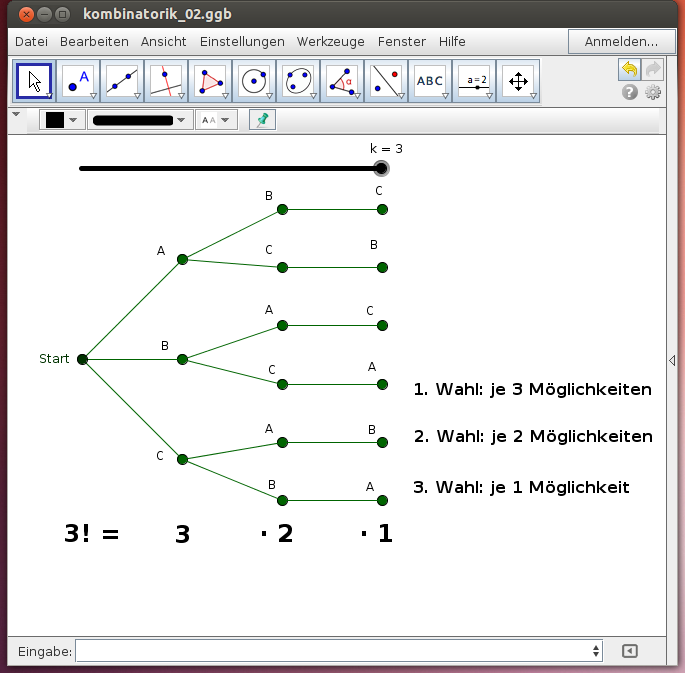
Permutation ohne Wiederholung
Gib alle Möglichkeiten an, aus den drei Buchstaben „A“, „B“ und „C“ einen dreistelligen Code zu bilden, wenn jeder Buchstabe nur einmal („ohne Wiederholung“) vorkommen soll!
Aufgaben:
- Gehe die Berechnung stufenweise mit dem Schieberegler für k durch und begründe die Berechnungsformel!
- Notiere alle verschiedenen Kombinationen der Buchstaben „A“, „B“ und „C“!
- Notiere alle verschiedenen Kombinationen der Buchstaben „A“, „B“, „C“ und „D“ und gib ihre Anzahl an!
- Begründe die allgemeine Formel: „Es gibt n! Permutationen ohne Wiederholung von n Objekten.“
Zurück zu Stochastik