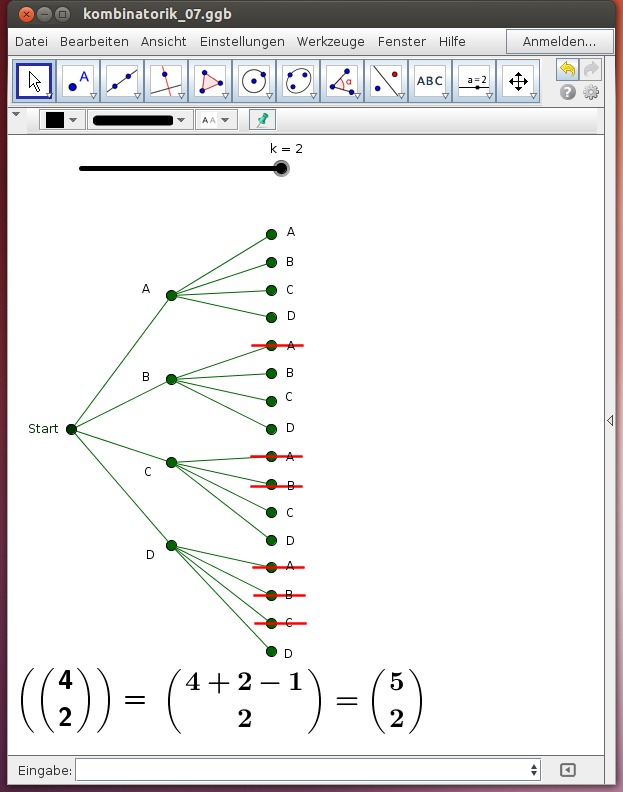
Kombination mit Wiederholung
Auf wie viele Arten können Gruppen von 2 Buchstaben aus den Buchstaben „A“, „B“, „C“ und „D“ - in beliebiger Reihenfolge, Buchstaben dürfen auch zweimal gewählt werden („mit Wiederholung“) - gebildet werden?
Aufgaben:
- Gehe die Berechnung stufenweise mit dem Schieberegler für k durch, begründe die Streichungen und die Berechnungsformel!
- Notiere alle Ergebnisse für die Zweier-Gruppen aus den Buchstaben „A“, „B“, „C“ und „D“!
- Die allgemeine Formel für die Berechnung aller Gruppen mit k Objekten, die aus n verschiedenen Objekten in beliebiger Reihenfolge gebildet werden können, ist:
. Dabei kann
,
oder auch
sein. Überprüfe die Gültigkeit dieser Formel für verschiedene Buchstabengruppen, z.B.
und
oder für
und
(Beachte: Die Buchstaben können mehrmals auftreten!)
Ausblick:
- Lies zu Multimengen nach!
Zurück zu Stochastik