Das Heron-Verfahren

tm.jpg 6, S. 54 - 55

Das Heron-Verfahren („babylonisches Wurzelziehen“) wurde in der Antike entwickelt; es dient zum Berechnen der Seitenlänge a eines Quadrates, von dem der Flächeninhalt A gegeben ist. tex:\sqrt A soll somit bestimmt werden.

  1. Beginne mit einem Startwert tex:l_0, der Länge eines flächengleichen Rechtecks.
  2. Bestimme die zugehörige Breite tex:b_0 = \frac A {l_0}
  3. Bilde den arithmetischen Mittelwert aus Länge und Breite: tex:\frac {l_0 + b_0} 2
  4. Dieser Mittelwert ist die Seitenlänge des nächsten Rechtecks …

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Beobachte, wie die Quadratwurzel bereits nach wenigen Iterationsschritten auf einige Dezimalstellen genau bestimmt wird!
  • Begründe die Formel B2 = A/A2!
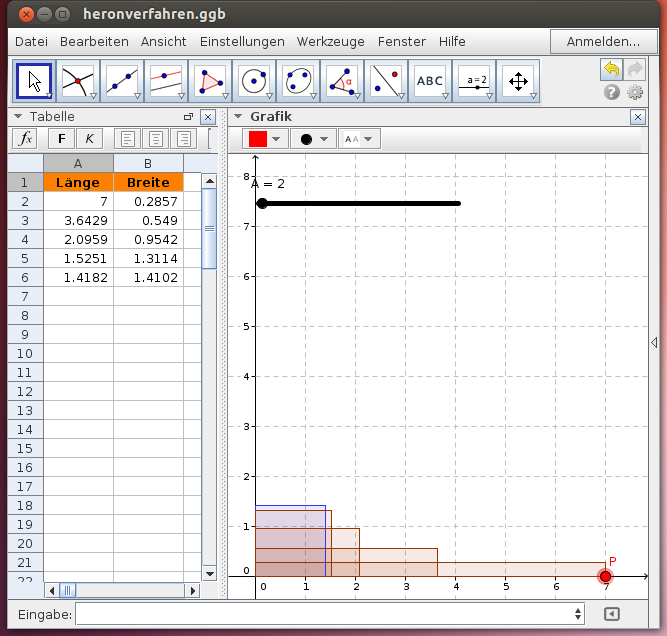
  • Begründe die Formel A3 = (A2 + B2)/2!
  • Im obigen Beispiel wurde die Quadratwurzel tex:\sqrt{A} = \sqrt{2} \approx 1.4182 näherungsweise bestimmt. Wähle mit dem Schieberegler für A verschieden große Quadrate und berechne ihre Seitenlängen mit dem Heronverfahren!
  • Gib die Rekursionsgleichung an!

Zurück zu Folgen und Reihen


Zuletzt angesehen: • heron-verfahren