Inhaltsverzeichnis
GPS - Global Positioning System
(zu 
7 S. 196 - 197)
Das gobale Satelliten-Navigationssystem dient zur (möglichst) genauen Bestimmung von Position und Zeit.
- Lies die geometrischen Grundlagen zum GPS in Thema Mathematik 7 nach (Thema: Kugeln)!
- Beschreiben: Welche Rolle spielt die Signallaufzeit von Satellit zu Empfänger?
- Lies zur genauen Zeitbestimmung beim GPS nach!
Weblinks
WikiPedia:
- http://de.wikipedia.org/wiki/Ortung (Ortsbestimmung)
- http://de.wikipedia.org/wiki/GPS (Global Positioning System)
- http://de.wikipedia.org/wiki/Galileo_%28Satellitennavigation%29 (Europäisches Satellitennavigationssystem Galileo)
Galileo
Aufgaben
- Recherchiere die historische Entwicklung von NAVSTAR-GPS!
- Recherchiere alternative Satelliten-Navigationssysteme!
- Zähle Aufgaben der Satelliten-Navigation in deinem Umfeld auf!
Berechnen von Schnittpunkten dreier Kugeln
Das Berechnen der beiden Schnittpunkte dreier Kugeln (falls diese existieren) ist ungewöhnlich …
- Unter welchen Voraussetzungen existieren überhaupt solche Schnittpunkte dreier Kugeln?
- In welchen Fällen existiert genau ein gemeinsamer Punkt dreier Kugeln?
- Berechne die Koordinaten der Schnittpunkte folgender Kugeln (Hinweis: Lies dazu die Anleitung in
7, S. 197):
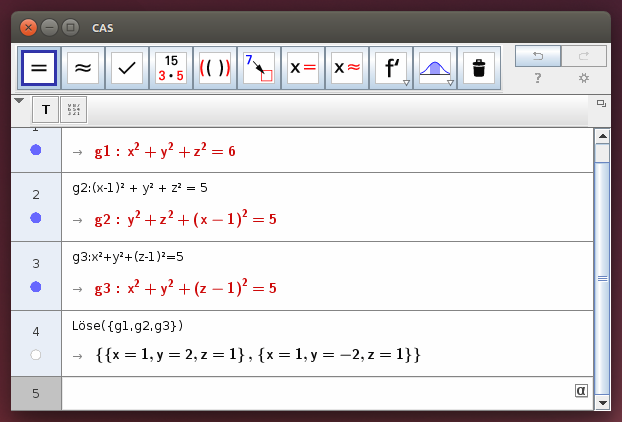
x² + y² + z² = 6 (x-1)² + y² + z ² = 5 x² + y² + (z-1)² = 5
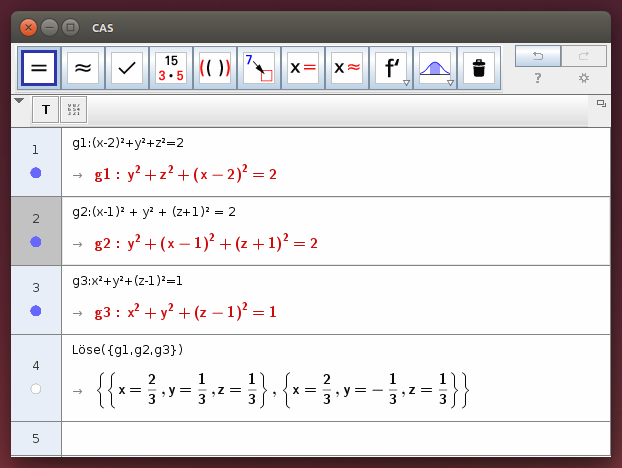
(x-2)² + y² + z² = 2 (x-1)² + y² + (z+1)² = 2 x² + y² + (z-1)² = 1
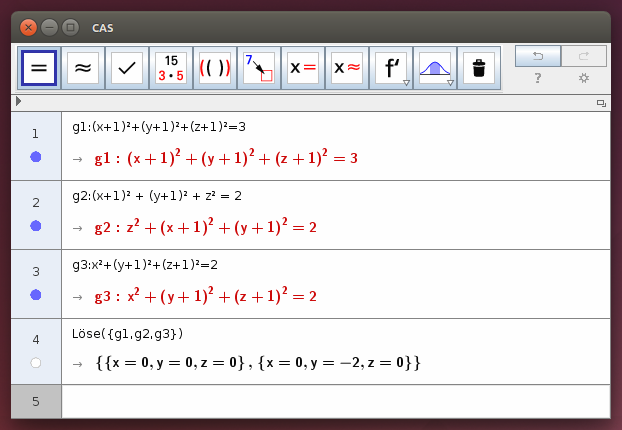
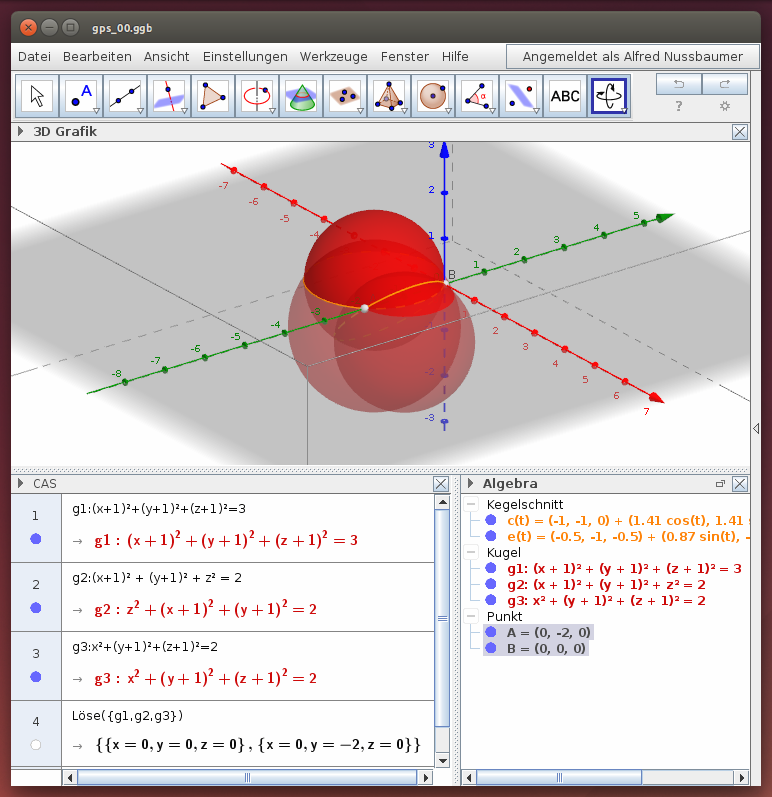
(x+1)² + (y+1)² + (z+1)² = 3 (x+1)² + (y+1)² + z² = 2 x² + (y+1)² + (z+1)² = 2
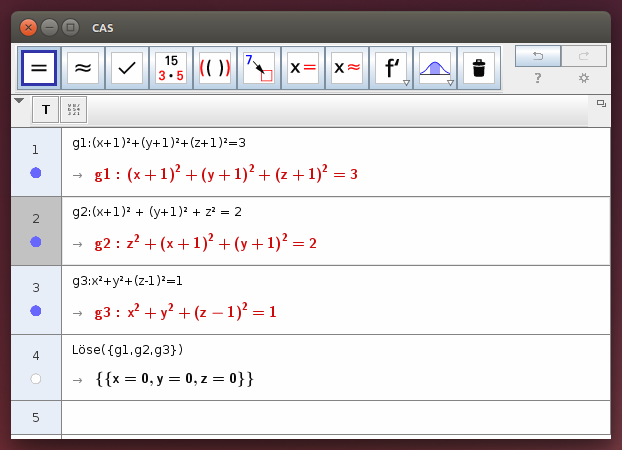
(x+1)² + (y+1)² + (z+1)² = 3 (x+1)² + (y+1)² + z² = 2 x² + y² + (z-1)² = 1
Hinweis: Darstellung und Schnitte von Kugelflächen mit GeoGebra
- Stelle die drei Kugelflächen in der 3D-Ansicht dar und bestimme die Schnittkreise zwischen den Kugelflächen!
- Bestimme die Schnittpunkte zwischen zwei Schnittkreisen!
- Vergleiche mit den Lösungen des Gleichungssystem im CAS!
Ausblick
- Forschung und Entwicklungsstand zum Europäischen Satelligennavigationssystem Galileo (vgl. obige Weblinks)
Studium
- Nachrichtentechnik
- Weltraumtechnik (Luft- und Raumfahrttechnik)
