Zurück zu: 5.Klasse » Analytische Geometrie der Ebene

Parameterform der Geradengleichung - Herleitung

zu Thema Mathematik 5 5, S. 210 - 211, zu BIFIE GK AG3.4

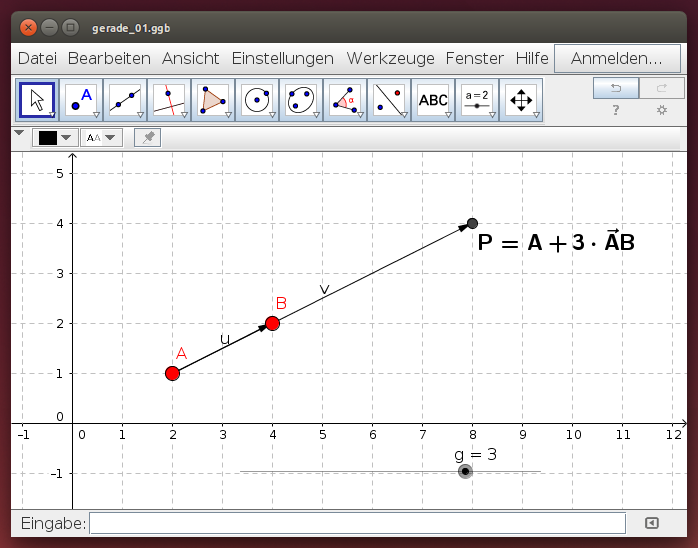
Du erreichst den Punkt P, indem du vom Punkt A ein Vielfaches des Vektors tex:\vec {AB} weitergehst: tex:P = A + g \cdot \vec {AB}.

Wähle verschiedene Werte für g mit dem Schieberegler und beobachte die Positionen des Punktes P:

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Überlege: Für welchen Wert von g gilt P = A? Überprüfe deine Antwort mit dem Applet!
  • Überlege: Für welchen Wert von g gilt P = B? Überprüfe deine Antwort mit dem Applet!
  • Überlege: Welche Auswirkungen hat das Vorzeichen von g in Hinblick auf die Lage von P?
  • Verschiebe die Punkte A und B in neue Positionen und überprüfe deine Antworten auf die obigen Fragen!
  • Vergleiche die Vektoren tex:\vec u = \vec {AB} und tex:\vec v = \vec {AP} und gib - je nach Position des Punktes P - Beziehungen an, z.B.: tex:\vec v = 3 \cdot \vec u

Zurück zu Analytische Geometrie der Ebene


Zuletzt angesehen: • gerade_01