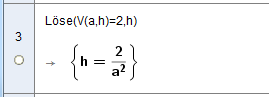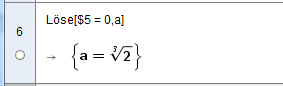Optimierungsaufgaben mit dem CAS lösen
Beispiel:
Ein quadratisches Prisma (Länge der Basiskante: a, Höhe h) hat ein Volumen von 2 Liter. Die Oberfläche des Prismas soll ein Minimum sein - berechne seine Abmessungen!
Lösung:
Wir stellen die Hauptbedingung, die Nebenbedingung(en) und die Zielfunktion auf, berechnen die Ableitungen und bestimmen so den Extremwert …
Hauptbedingung und Nebenbedingung aufstellen:
Beachte: Formeln mit mehr als 1 Variable werden farblich hervorgehoben. Sie können in der Version 4 nicht dargestellt werden.
Eine Variable aus der Nebenbedingung freistellen
Beachte: Das gegebene Volumen des Prismas führt zur Gleichung V(a,h)=2. Wir lösen die Gleichung für die Variable h.
Die Zielfunktion aufstellen
Beachte: Die Zielfunktion hat nur mehr eine Variable. Sie wird als Funktionsgraph im Grafikfenster dargestellt. Wir erhalten die Zielfunktion mit dem Befehl Ersetze(<Ausdruck>, <Substitutionsliste>). Beachte die dynamischen Zeilenbezüge!
Erste Ableitung bilden
Die Nullstellen der ersten Ableitung bestimmen
Alle Abmessungen bestimmen
Wir setzen die Lösung der einen Variablen in die andere Variable ein … Beachte die Verwendung des Befehls Ersetze(<Ausdruck>,<Substitutionsliste>) und die dynamischen Zeilenbezüge!
Aufgaben:
- Wähle andere Vorgabewerte für das Volumen des quadratischen Prismas und interpretiere die Ergebnisse der Abmessungen
Zurück zu AN3.3