Inhaltsverzeichnis
Kurven und Flächen
Kurven in impliziter Darstellung
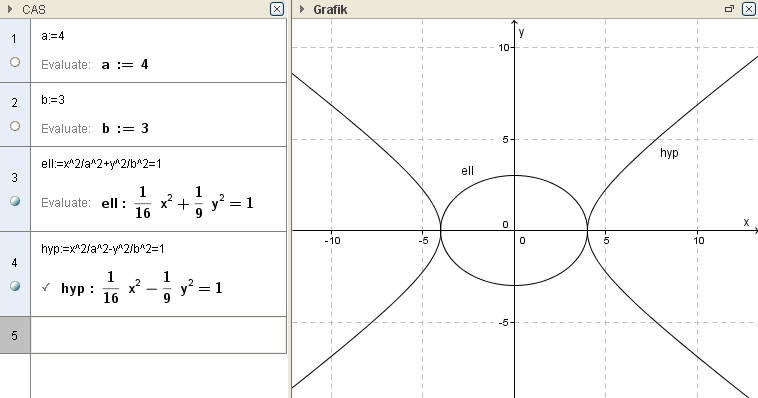
Kurven können in implziter Darstellung eingegeben werden und werden in dieser Darstellung auch geplottet
Ex: Stelle die Ellipse und die Hyperbel mit $a = 4$ und $b = 3$ graphisch dar.
Weiter zu Elliptische Kurven
Kurven in Parameterdarstellung
Mit Befehl Kurve
In der Ebene und im Raum werden Parameterkurven durch $X(t) =\dbinom {x(t)} {y(t)}$ bzw. durch $X(t) = \left(\begin{matrix} x(t)\\ y(t)\\ z(t) \end{matrix}\right)$ mit $t \in [a;b]$ beschrieben.
Für die Darstellung steht der Befehl Kurve(<Ausdruck>, <Ausdruck>,
<Parameter>, <Startwert>, <Endwert>) zur Verfügung.
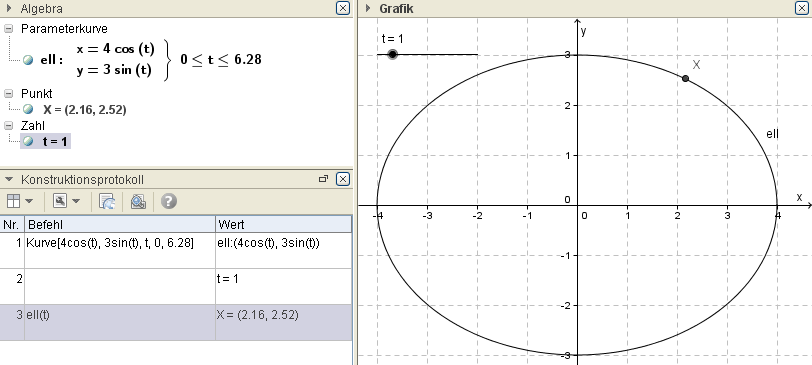
Ex: Gib die Parameterdarstellung der Ellipse mit a=4 und b=3 an
$X(t) =\dbinom {4\cdot\cos(t)} {3\cdot\sin(t)}$, $0 ≤ t ≤ 2\pi $
Spur eines wandernden Punktes
Kurven entstehen durch die Wanderung eines Punktes auf einer Bahn. Dies lässt sich sehr schön auch ohne den Befehl Kurve umsetzen. Es genügt dazu einfach einen Punkt X abhängig von einem Parameter (als Schieberegler) wandern zu lassen.
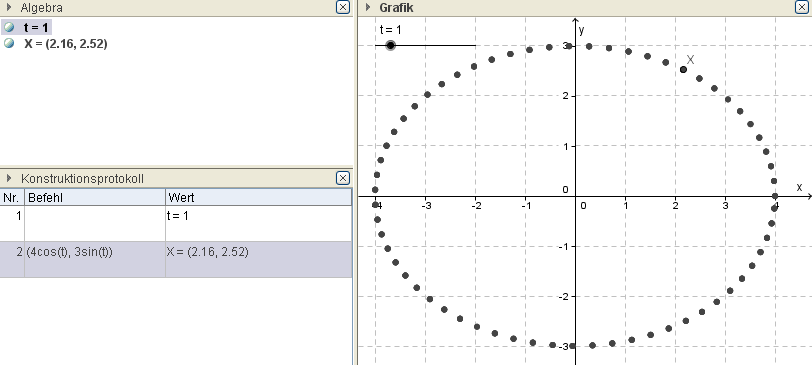
Ex: Gib die Parameterdarstellung der Ellipse mit a=4 und b=3 ohne den Befehl Kurve an.
$X(t) =(4\cdot\cos(t),3\cdot\sin(t))$, $0 ≤ t ≤ 2\pi $
Ortslinie eines wandernden Punktes
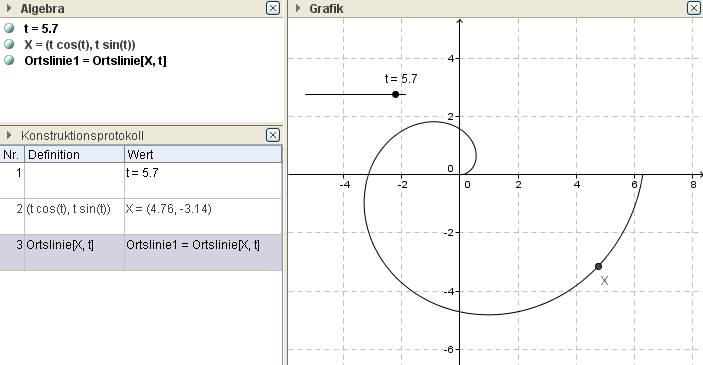
Ex: Erzeuge mit Hilfe eines wandernden Punktes eine Ortslinie einer Spiralbahn. Diese entseht indem wir bei der Parameterdarstellung eines Kreise kontinuierlich den Radius vergrößern.
Spirale $X(t) =\dbinom {t\cdot\cos(t)} {t\cdot\sin(t)}$, $0 ≤ t ≤ 2\pi $ .
Kurven im Raum
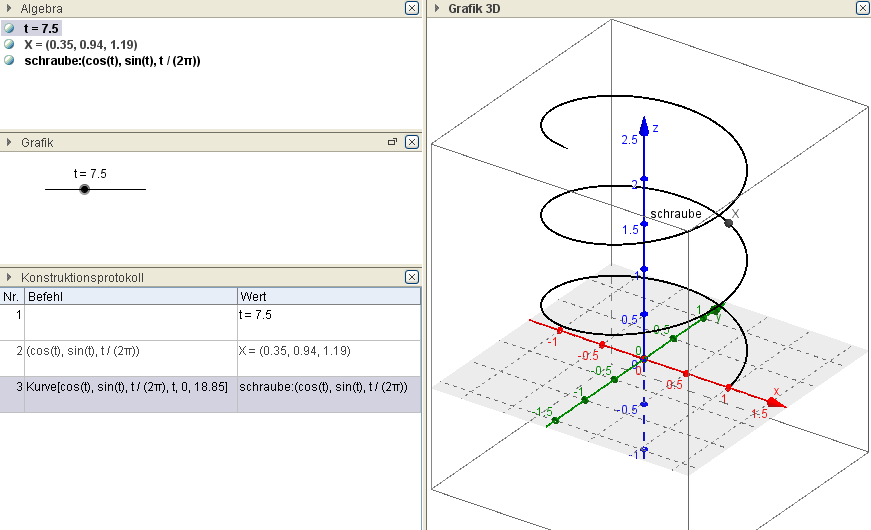
Ex: Erzeuge eine (interaktive) Darstellung der Schraubenlinie, die durch folgende Parameterdarstellung gegeben ist.
$X(t) = \left(\begin{matrix} \cos(t)\\ \sin(t)\\ \frac{t}{2\pi} \end{matrix}\right)$ mit $t \in [0;6\pi]$
Kurven in Polardarstellung
Ex: Stelle die lineare Funktion $f(\varphi) = \frac{\varphi}{5} +1 $ für $0\leq \varphi < 6\pi$ in Polardarstellung dar!
Hinweis: Da Geogebra zwar das Koordinatensystem in Polardarstellung anzeigen kann, nicht aber Funktionen in Polardarstellung interpretieren kann, muss dies mit $f(\varphi)\cdot\binom{\cos(\varphi)}{\sin(\varphi)}$ selbst erledigt werden.
Flächen
Ähnlich wie Kurven können wir auch Flächen im Raum unter Verwendung von Parametern darstellen. Da es meist schwierig ist, derartige Flächen auch nur zu skizzieren, ist der Einsatz eines Computeralgebrasystems mit entsprechenden grafi schen Möglichkeiten unumgänglich.
Die Parameterdarstellung $X (u, v) = \left(\begin{matrix} x(u,v)\\ y(u,v)\\ z(u,v)\end{matrix}\right)$, $u \in [a; b], v \in [c; d]$, weist jedem Paar von Parameterwerten $u,v$ eindeutig einen Punkt P im Raum zu. Es entsteht dabei eine Fläche im Raum.
Ex: Kugelfläche
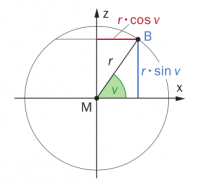 Zur Herleitung der Parameterfläche einer Kugel können wir uns die Kugel aus Breitenkreislinien zusammengesetzt vorstellen. Wenn $r$ der Radius der Kugel ist, dann ergibt sich für den Radius $R$ des Breitenkreises: $R = r\cdot cos v$.
Der Breitengrad wird dabei durch den Winkel $v$ angegeben. Da der Breitenkreis in der Höhe $z = r \cdot sin v$ liegt, ergibt sich somit:
Zur Herleitung der Parameterfläche einer Kugel können wir uns die Kugel aus Breitenkreislinien zusammengesetzt vorstellen. Wenn $r$ der Radius der Kugel ist, dann ergibt sich für den Radius $R$ des Breitenkreises: $R = r\cdot cos v$.
Der Breitengrad wird dabei durch den Winkel $v$ angegeben. Da der Breitenkreis in der Höhe $z = r \cdot sin v$ liegt, ergibt sich somit:
$X(u,v) = \left( \begin{matrix} r\cdot \cos(v)\cdot cos(u)\\ r\cdot\cos(v)\cdot cos(u)\\ r\cdot \sin(v) \end{matrix}\right )$, $u \in [0; 2\pi[, v \in [-\pi/2; \pi/2]$