Der Flächeninhalt unter der Kettenlinie
Die Kettenlinie beschreibt die Form einer Kette, die sie aufgrund ihres Eigengewichts einnimmt, wenn sie zwischen zwei (horizontalen) Punkten aufgehängt ist.
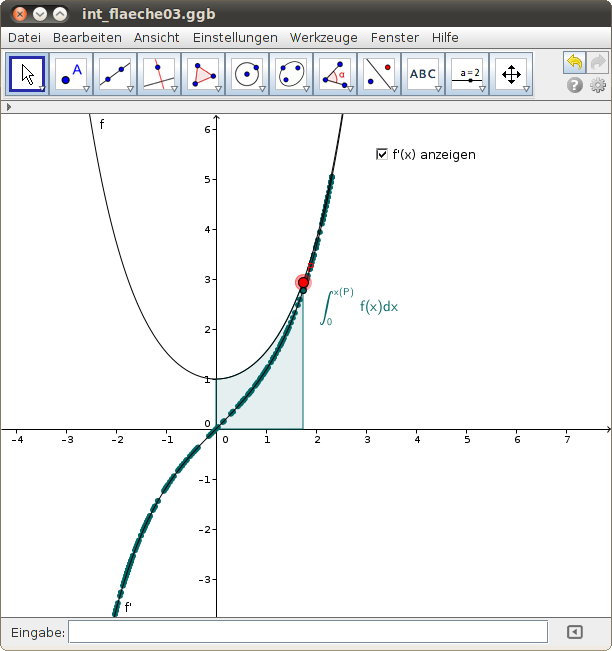
Im folgenden Beispiel betrachten wir die Kettenlinie und den Flächeninhalt unter f(x) zwischen 0 und der rechten Grenze x(P). Verschiebe diese rechte Grenze, indem du den roten Punkt P auf dem Funktionsgraphen von f(x) verschiebst:
Aufgaben:
- Der Wert des Integrals wird als Funktion der rechten Grenze in Form einer Punktespur dargestellt. Beschreibe ihre Form!
- Vergleiche diese Funktion des Flächeninhalts mit der 1. Ableitung f'(x)!
- Ausblick: Vergleiche den Flächeninhalt unterhalb der Kettenlinie mit ihrer Bogenlänge!
Zurück zu Flächeninhalt unter einer Kurve | Anwendungen der Integralrechnung