Inhaltsverzeichnis
Prismen und Pyramiden mit Ebenen schneiden
Für die folgenden Überlegungen betrachten wir Quader, Pyramiden und Doppelpyramiden. Wir schneiden diese Körper mit ebenen Flächen und erhalten jeweils zwei Teilkörper. Wir besprechen jeweils einen dieser Teilkörper und beschreiben die Schnittfläche.
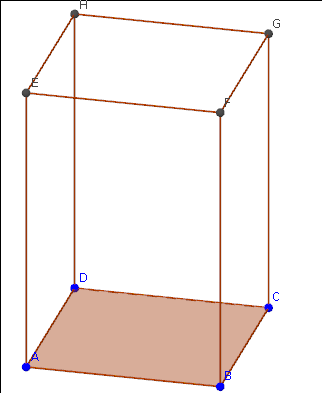
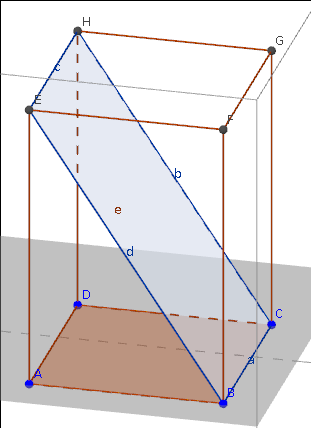
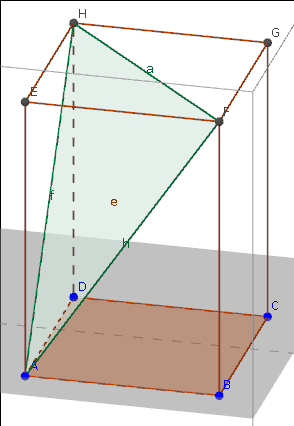
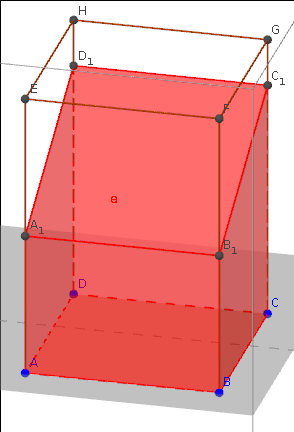
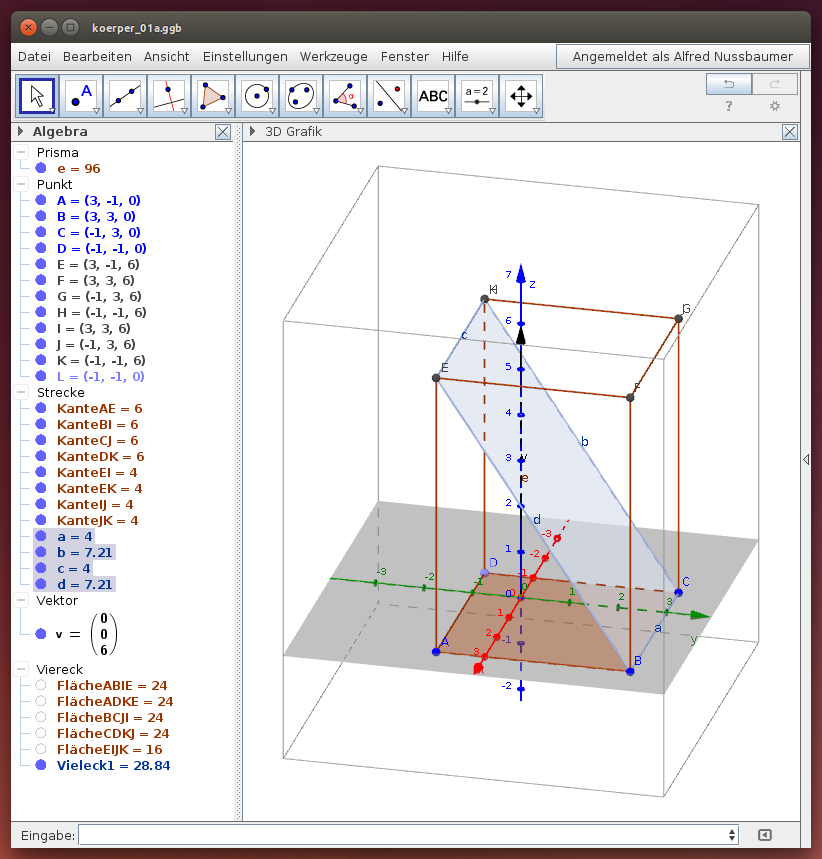
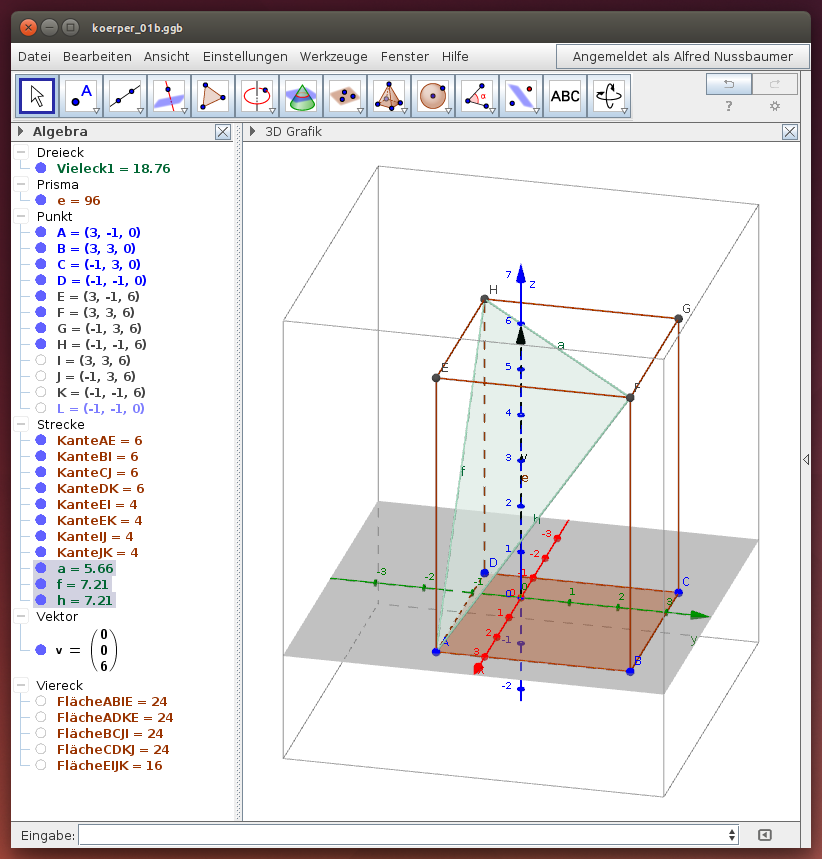
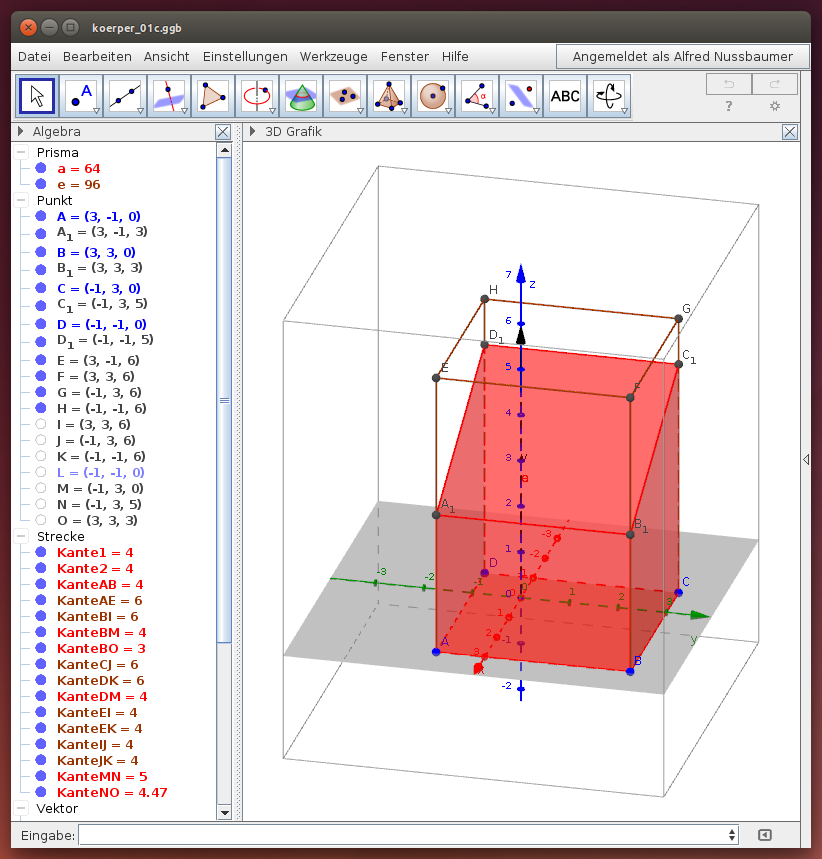
Quader
Aufgabe 1:
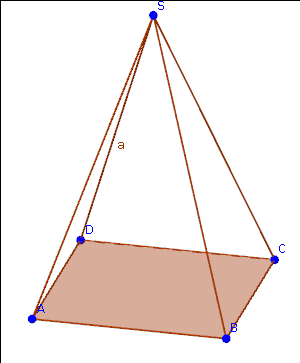
Quadratische Pyramide
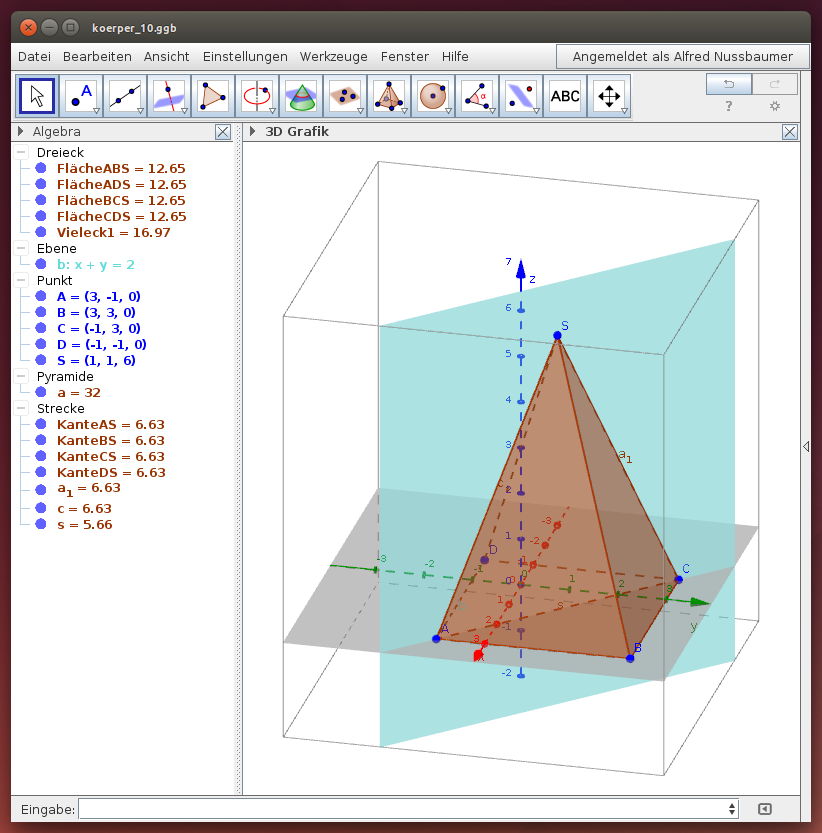
Aufgabe 2:
Die Eckpunkte ABCD einer quadratischen Pyramide haben die Koordinaten A(-3|-1|0), B(3|3|0), C(-1|3|0), D(-1|-10) und die Spitze S(1|1|6). Berechne den Flächeninhalt der Schnittfläche, die durch die Flächendiagonale AC und die Spitze S gegeben ist, und das Volumen des Teilkörpers!
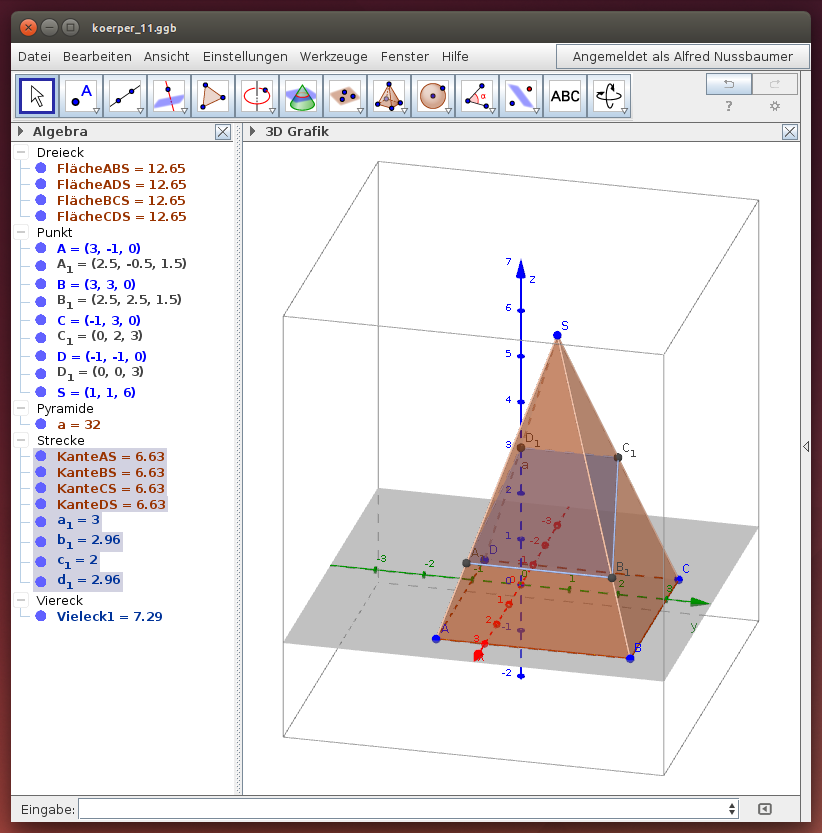
Aufgabe 3:
Die Eckpunkte ABCD einer quadratischen Pyramide haben die Koordinaten A(-3|-1|0), B(3|3|0), C(-1|3|0), D(-1|-10) und die Spitze S(1|1|6). Die Teilungspunkte teilen die Kanten der Pyramide im Verhältnis 1 : 1 oder 1 : 3. Berechne die Koordinaten der Eckpunkte der Schnittfläche!
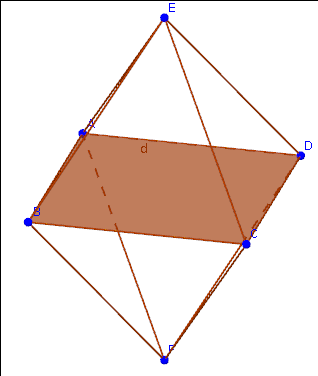
Doppelpyramide
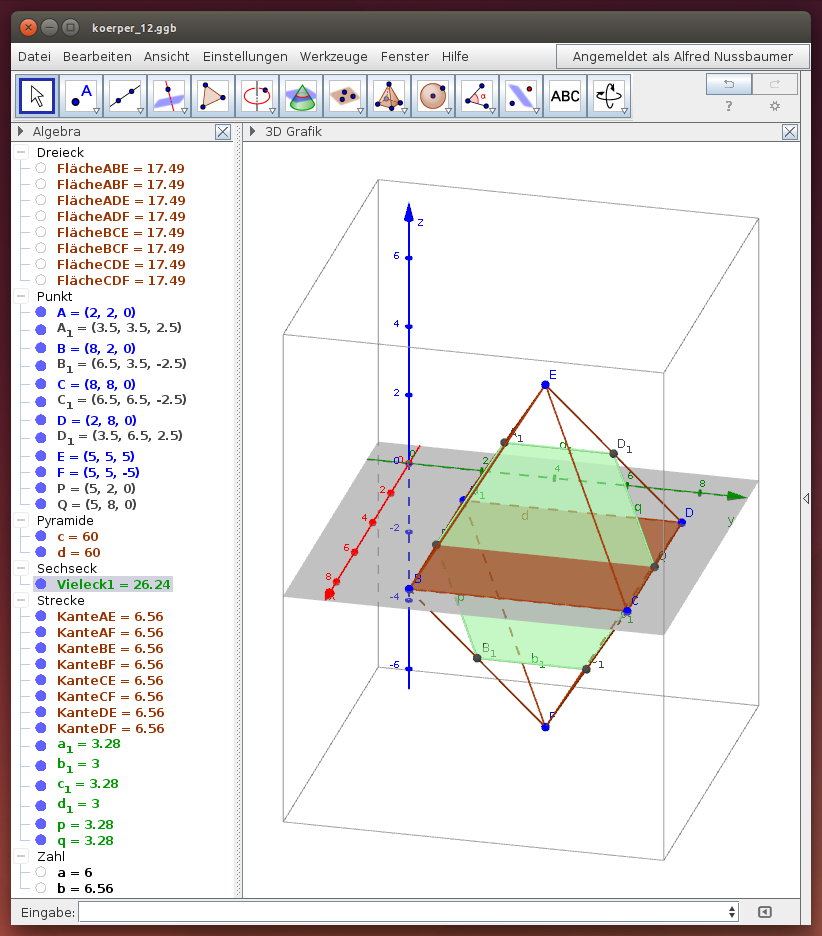
Aufgabe 4:
Die Eckpunkte ABCD des Oktaeders haben die Koordinaten A(2|2|0), B(8|2|0), C(8|8|0), D(2|8|0) und die beiden Spitzen E(5|5|5) und F(5|5|-5). Eine Schnittebene teilt das Oktaeder so, dass sechs Kanten halbiert werden.
- Zeige, dass kein regelmäßiges Oktaeder vorliegt!
- Zeige, dass die Schnittfigur kein regelmäßiges Sechseck ist!
Weitere Aufgaben
- Rechne nach, wie sich eine gleichseitige dreiseitige Pyramide aus den Eckpunkten eines Würfels bilden lässt! Bestimme die Kantenlänge dieses Tetraeders, wenn die Kantenlänge des Würfels a ist!
- Rechne nach und überprüfe, ob es sich bei den dargestellten Schnittfiguren tatsächlich um ein Quadrat und um ein gleichseitiges Dreieck handelt! Gibt es weitere Möglichkeiten?
- Untersuche die Eigenschaften und ebenen Schnitte der weiteren „platonischen Körper“ (Oktaeder, Dodekaeder, Ikosaeder)!
Anwendungen in der Architektur
Recherchiere, wo Würfel, Quader oder Pyramiden in der Architektur verwendet werden! Kommen hier ebene Schnitte mit diesen Körpern vor?
Ausblick
- Ebene Schnitte von Kreiszylindern
- Kegelschnitte
- Ebene Schnitte von Kugeln
Studium
- Darstellende Geometrie
- Architektur
Zurück zu 6. Klasse