Lernpfad Maxima: Flächen in Parameterdarstellung

Bei diesem Lernpfad erarbeitest du das Grundlagenwissen um Flächen in Parameterdarstellung im R³. Alle diese Flächen werden durch zwei Parameter beschrieben.

Wenn du mit dem Maxima-Befehl plot3d noch nicht vertaut bist, arbeite zuerst den Lernpfad dazu durch!

Die Flächen kannst du beispielsweise mit maxima darstellen - mach dich im ersten Schritt mit einigen Befehlen vertraut!

Die Ebenengleichung in Parameterform erlaubt die Beschreibung von Ebenen im R³ mit Hilfe eines Einstigspunktes („Anfangspunkt“) und mit Hilfe zweier Richtungsvektoren mit jeweils einem Parameter. Dabei hängt jede Koordinatenfunktion diesen zwei Parametern ab, z.B.:

x(u,v) = 1 + u +  v
y(u,v) =   - u + 2v
z(u,v) = 1     +  v

Mit geeigneten Funktionen für diese Koordinaten erhältst du eine Reihe von Flächen, z.B.: Zylinderfläche, Kegelfläche, Kugel …

Aufgaben:

Lies im Artikel Kurven und Flächen im Raum nach!

Untersuche folgende Flächen, vergleiche mit den Grundaufgaben und erkläre die Darstellungen! Welche Eigenschaften haben die Flächen? Variiere auch die angegebenen Konstanten, beobachte und beschreibe ihre Bedeutung auf die Form der Fläche.

Bestimme fallweise die „Parameterlinien“ für u = const. und v = const.!

x(u,v) = 2 v
y(u,v) = cos(u)
z(u,v) = sin(u)

x(u,v) = cos(u) * 3 v
y(u,v) = sin(u) * 2 v
z(u,v) = 4 v

x(u,v) = cos(u) * sqrt(36 - v^2)
y(u,v) = sin(u) * sqrt(36 - v^2)
z(u,v) = -v

x(u,v) = cos(u) * 3 * sqrt(v^2 - 1)
y(u,v) = sin(u) * 2 * sqrt(v^2 - 1)
z(u,v) = 4 v

x(u,v) = cos(u) * 3 * sqrt(1 + v^2)
y(u,v) = sin(u) * 2 * sqrt(1 + v^2)
z(u,v) = 4 v

x(u,v) = u^2 * v
y(u,v) = u * v^2
z(u,v) = u * v

x(u,v) = u
y(u,v) = v
z(u,v) = x^2 + v^2

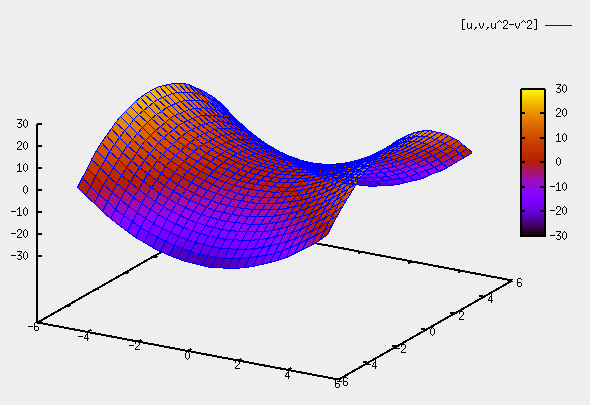
Untersuche die Eigenschaften der Sattelfläche:

x(u,v) = u
y(u,v) = v
z(u,v) = u * v

x(u,v) = u + v
y(u,v) = u - v
z(u,v) = u * v

x(u,v) = u
y(u,v) = v
z(u,v) = u^2 - v^2

Untersuche die Eigenschaften der Wendelfläche:

x(u,v) = cos(u) * v
y(u,v) = sin(u) * v
z(u,v) = 6 u

Hinweis:

Die Parameterdarstellung von Flächen ist eine Abbildung vom R² in den R³