Inhaltsverzeichnis
Schnittpunkt von 3 Ebenen
Im Allgemeinen haben drei Ebenen einen Punkt gemeinsam (Schnittpunkt).
Beispiel: Berechne den Schnittpunkt der drei Ebenen e1: x +2y - z = 1, e2: 3x + y + 2z = 3, e3: 2x - y + 4z = 2!
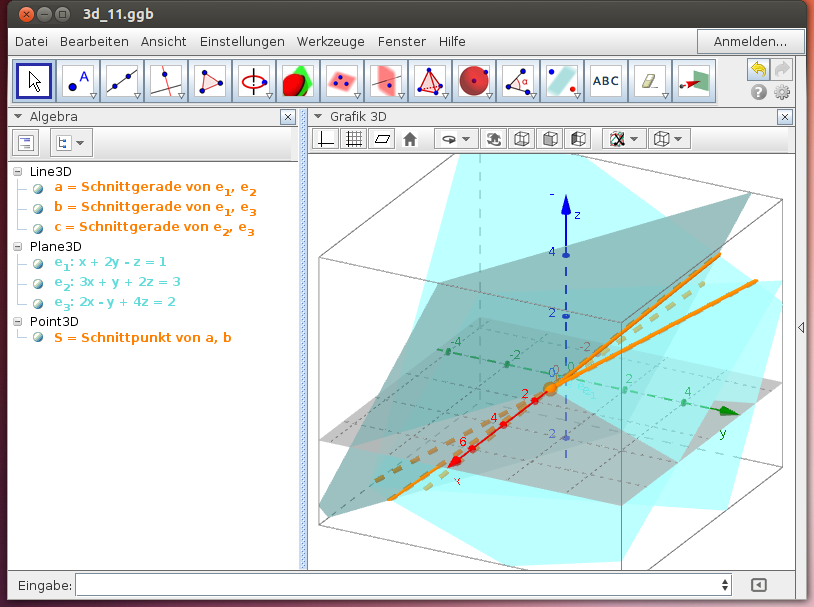
Lösung in der Grafikansicht Grafik 3D
Gib die drei Ebenengleichungen in Normalvektorform als Gleichungen in den drei Variablen x, y und z ein, bestimme jeweils die Schnittgeraden zweier Ebenen und schließlich den Schnittpunkt als Schnitte zweier Schnittgeraden:
Ergebnis: S(1|0|0)
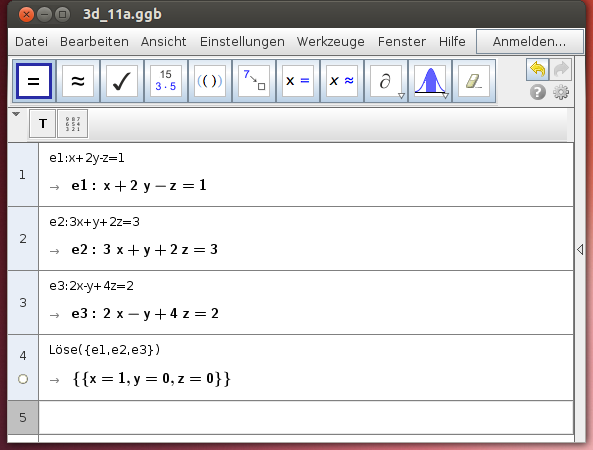
Lösung mit dem CAS
Gib die drei Ebenengleichungen als lineare Gleichungen in den Unbekannten x, y und z ein und löse das lineare Gleichungssystem!
Ergebnis: S(1|0|0)
Aufgaben:
- Untersuche Lagebeziehungen weiterer Ebenen und beschreibe insbesondere die Lösungen, wenn Ebenen parallel oder identisch sind!
Zurück zu Analytische Geometrie des Raumes