Drei Wege zum Ziel

Technologien ermöglichen meist drei verschiedene Bearbeitungs-Zugänge im Mathematikunterricht:

Geometrisch/konstruktiver Zugang: Das gewünschte Problem wird (unter Einsatz der entsprechenden Werkzeuge) in der Graphikansicht bearbeitet. Gleichzeitig entsteht im Algebrafenster ein „numerisches Protokoll“.

• Beispiel 1: Konstruktion des Umkreises
• Beispiel 2: Konstruktion einer Tangente an eine Funktion

Strategisch/analytischer Zugang: Das gewünschte Problem wird (durch Angabe der enstreckenden Befehle) im Algebrafenster. Gleichzeitig entsteht im Graphikfenster ein „graphisches Protokoll“. Da die einzelnen Problemlöseschritte in Form von Befehlen zur Verfügung stehen (z.B. Streckensymmetrale(A,B) oder Tangente(f,P)) bleiben die Details der Berechnung „Black Boxes“.

• Beispiel 1: Strategie zur Berechnung/Konstruktion des Umkreises
• Beispiel 2: Strategie zur Berechnung/Konstruktion einer Tangente an eine Funktion

Rechnerisch/analytischer Zugang: Das gewünschte Problem wird schrittweise im Algebra-Fenster oder in der CAS-Umgebung gelöst. Gleichzeitig entsteht „numerisches/algebraisches Protokoll“ (Konstruktionsprotokoll oder CAS-Fenster) und im Graphikfenster ein „graphisches Protokoll“. Dies entspricht am ehestender „händischen Berechnung“, im Unterschied zu dieser sollte es aber zu keinen Rechenfehlern kommen oder dazu dass die Bearbeitung eingestellt wird, da der Rechenaufwand zu groß oder kompliziert wird.

• Beispiel 1: Berechnung des Umkreises
• Beispiel 2: Berechnung einer Tangente an eine Funktion

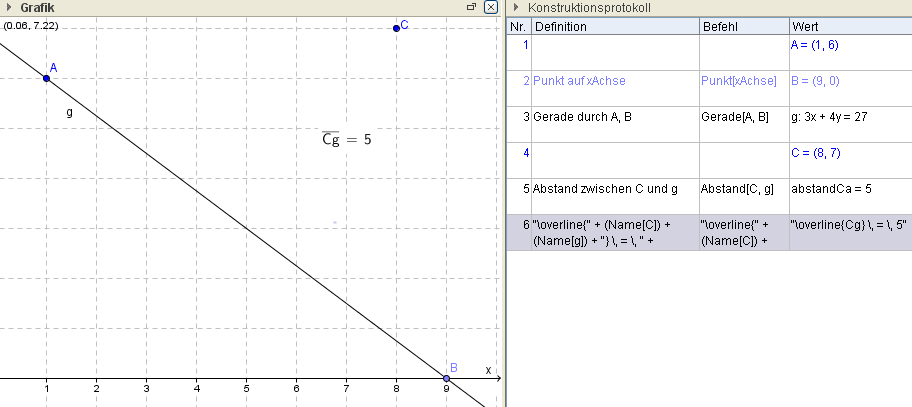
Ex: Berechne den Abstand des Punktes P=(8|7) von der Geraden g[A=(1|6),B=(9|0)]

a) Geometrisch

b) Strategisch

c) Algebraisch