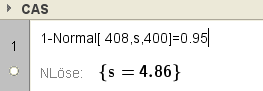Inhaltsverzeichnis
Wahrscheinlichkeitsrechnung
Grundaufgaben zur Binomialverteilung
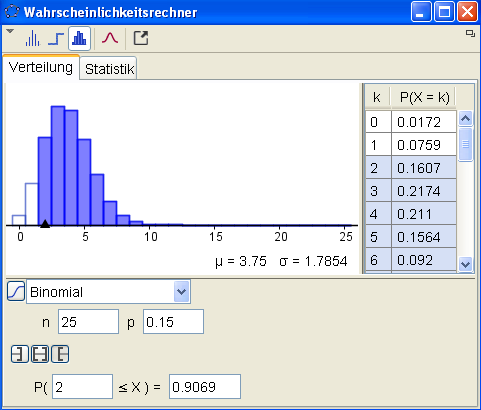
Ex: Bei einer Impfung treten im Mittel bei 15 von 100 Personen leichte Gegenreaktionen auf.
Es wird eine Schulklasse mit 25 SchülerInnen geimpft. Berechne die Wahrscheinlichkeit, dass
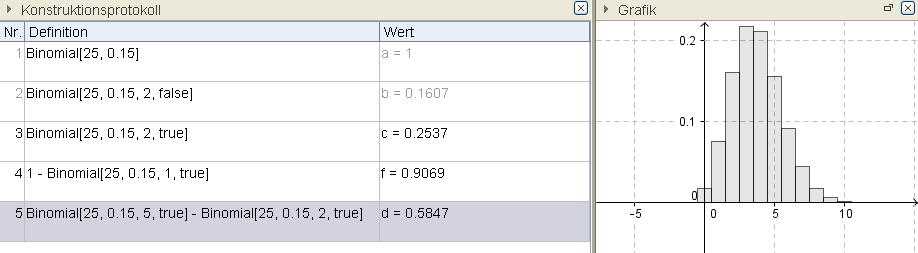
a) bei genau zwei SchülerInnen eine Gegenreaktion auftritt,
b) bei mindestens zwei SchülerInnen eine Gegenreaktion auftritt,
c) drei bis fünf SchülerInnen eine Gegenreaktion zeigen.
Mit Befehl: Binomial[25, 0.15, 2, false]
Mit Befehl: 1- Binomial[25, 0.15, 1, true]
Mit Befehl: Binomial[25, 0.15, 5, true] - Binomial[25, 0.15, 2, true]
Grundaufgaben zur Normalverteilung
Bei der Behandlung der Normalverteilung treten üblicherweise folgende Grundaufgaben auf:
(a) Berechnung von Wahrscheinlichkeiten (Berechnung von α bzw. γ),
(b) Berechnung von Intervallen zu vorgegebenen Wahrscheinlichkeiten (Berechnung von x),
(c) Berechnung von symmetrischen Intervallen zu vorgegebenen Wahrscheinlichkeiten (Berechnung von ε),
(d) Berechnung des Erwartungswertes (Berechnung von μ),
(e) Berechnung der Standardabweichung (Berechnung von σ).
Berechnung von Wahrscheinlichkeiten
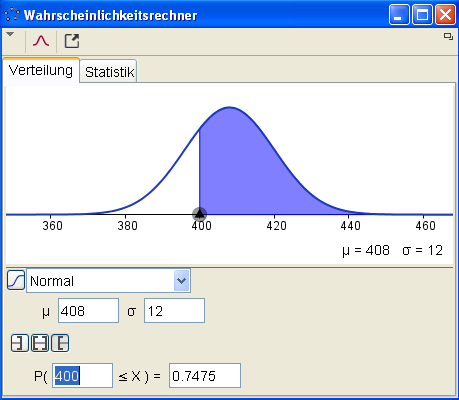
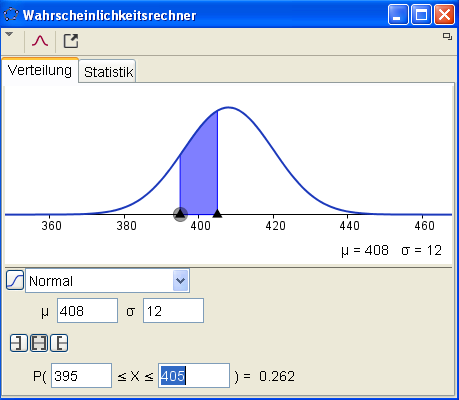
Ex: Ein Wiener Schnittenfabrikant füllt Packungen ab, deren Gewicht normalverteilt ist mit einem mittleren Wert von 408g und einer Standardabweichung von 12g.
Ex `a_1`: Welcher Prozentsatz der Packungen wiegt mindestens 400g ?
Ex `a_2`: Welcher Prozentsatz der Packungen wiegt zwischen 395g und 405g ?
Mit Befehlen:
- Normal(m,s,x) … Verteilungsfunktion zur Normalverteilungsfunktion mit den Parametern $\mu$ und $\sigma$.
Mit selbstdefinierter Verteilungsfunktion $P(\mu,\sigma,u_g,o_g)$:
Berechnung von Intervallen zu vorgegebenen Wahrscheinlichkeiten
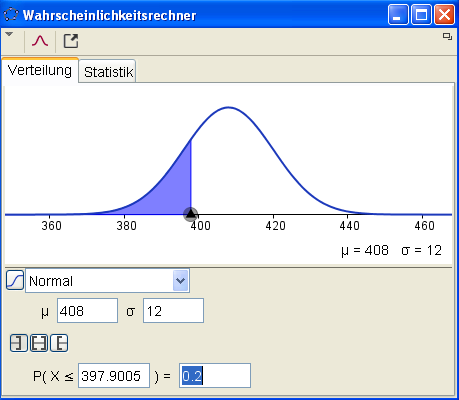
Ex: b) Wie viel wiegen die leichtesten 20% ?
Mit Befehlen:
Hinweis: Die numerische Berechnung mittels NSolve() benötigt einen Startwert (der in der Nähe des vermuteten Ergebnisses liegen sollte).
Mit selbstdefinierter Verteilungsfunktion $P(\mu,\sigma,u_g,o_g)$:
Berechnung von symmetrischen Intervallen zu vorgegebenen Wahrscheinlichkeiten
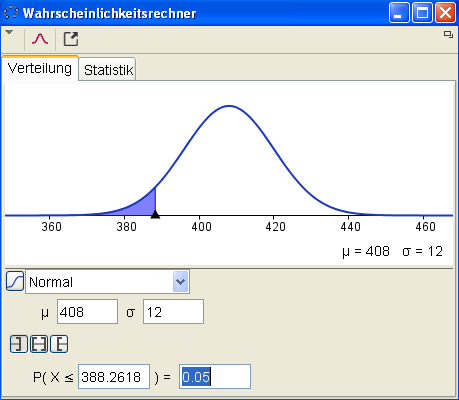
Ex: c) In welchem Gewichtsbereich befinden sich 90% der Packungen ?
Mit Befehlen:
Mit selbstdefinierter Verteilungsfunktion $P(\mu,\sigma,u_g,o_g)$:
Berechnung des Erwartungswertes
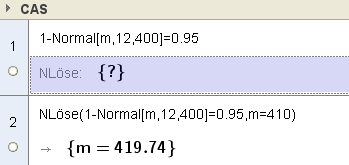
Ex: d) Der Schnittenfabrikant möchte garantieren, dass 95% der Packungen ein Mindestgewicht von 400g besitzen. Auf welchen Mittelwert ist die Abfüllanlage einzustellen ?
Hinweis: Die numerische Berechnung mittels NSolve() benötigt einen Startwert (der in der Nähe des vermuteten Ergebnisses liegen sollte).
Mit selbstdefinierter Verteilungsfunktion $P(\mu,\sigma,u_g,o_g)$:
Berechnung der Standardabweichung
Ex e) Der Schnittenfabrikant ist mit seiner Anlage nicht zufrieden. Eine neue Abfüllanlage mit einer geringeren Standardabweichung soll angeschafft werden. Diese soll bei einer Einstellung der mittleren Abfüllmenge auf 408g gewährleisten, dass mindestens 95% ein Gewicht von 400g aufweisen. Wie groß darf die Standardabweichung nun sein ?
Mit Befehl:
Mit selbstdefinierter Verteilungsfunktion $P(\mu,\sigma,u_g,o_g)$: