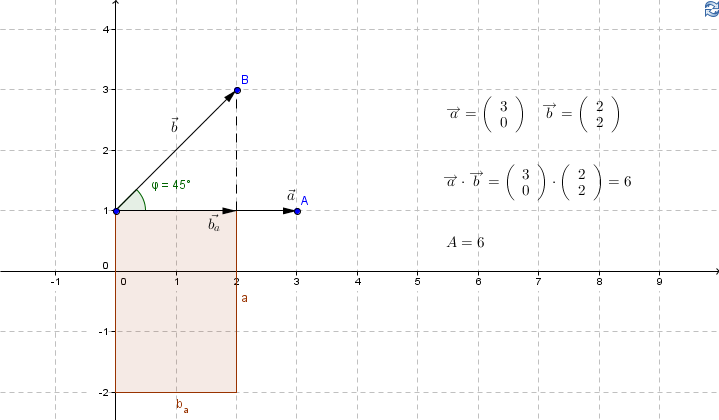Punkte und Vektoren
Vektoren mit mehr als 2 Komponenten werden als Listen eingegeben. Diese werden im Algebrafenster und in der CAS-Ansicht verschieden behandelt.
Grundlegendes zur Punkte und Vektoren
Nützliche Befehle
- Vektor(P) … Erzeugt einen Vektor zum Punkt P
- Vektor(<Anfangspunkt>,<Endpunkt) … Erzeugt einen Vektor zwischen den Punkten mit Anfangspunkt A und Endpunkt B
- Länge(v) … Gibt den Betrag des Vektors v an
- Einheitsvektor(v) … Erzeugt einen Einheitsvektor zum Vektor v, zur Geraden g oder zur Strecke s
- Normalvektor(v) … Erzeugt einen Normalvektor zum Vektor v, zur Geraden g oder zur Strecke s
- Einheitsnormalvektor(v) … Erzeugt einen Einheitsnormalvektor zum Vektor v, zur Geraden g oder zur Strecke s
- Winkel(u,v) … Berechnet den Winkel zwischen dem Vektor u und v (bemessen im mathematisch positiven Sinn)
- Beziehung(u,v) … Prüft die Vektoren u und v auf lineare Abhängigkeit
Eingabe von Punkten und Vektoren
- Großbuchstaben bezeichnen Punkte, Kleinbuchstaben hingegen Vektoren,
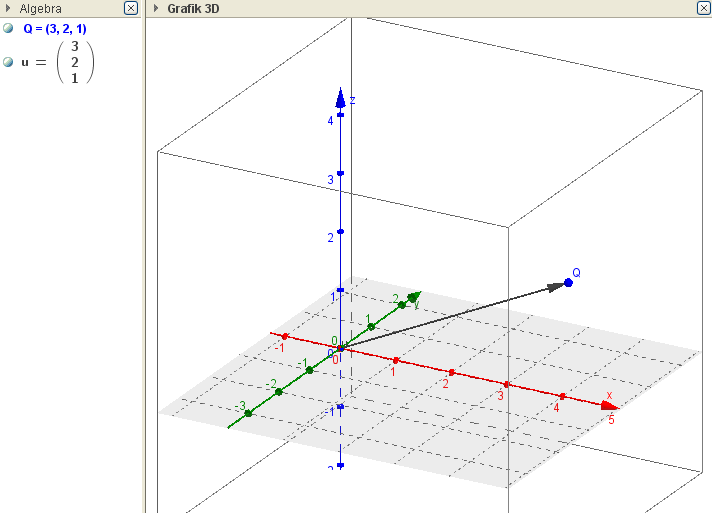
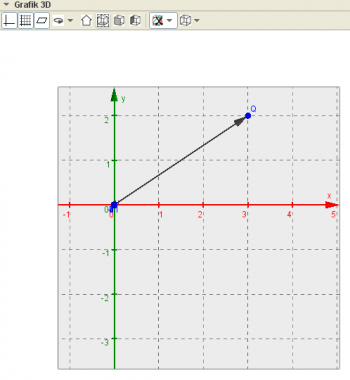
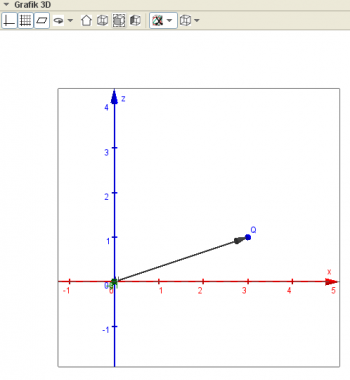
z.B. P = (1, 2) oder v = (0, 3) im $\mathbb{R}^2$ bzw. Q = (1, 2,3) oder $\vec u$ = (0, 3, 5) im $\mathbb{R}^3$
Ex: Stelle den Punkt Q =(1|2|3) und den Vektor $\vec u$ = (0, 3, 5) in der 3D-Ansicht dar und erzeuge die Projektionen in die 3 Koordinatenebenen!
Kartesische Koordinaten und Polarkoordinaten
- Sollen Polarkoordinaten eingegeben werden, so wird ein Strichpunkt zur Trennung von Radius und Winkel verwendet P = (1; 0°) oder v = (5; 90°).
- Zwischen kartesischer Darstellung und Polardarstellung kann (über die rechte Maustaste) umgeschaltet werden.
Addition/Subtraktion von Punkten und Vektoren
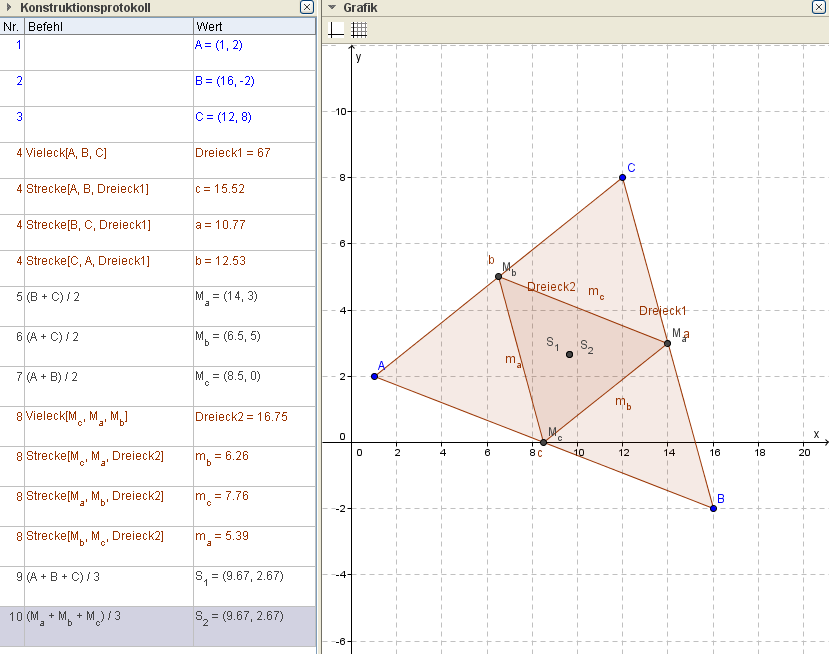
Ex: Ermittle im Dreieck ABC [A=(1|2),B=(16|-2),C=(12|8)] die Seitenmittelpunkte M_a, M_b, M_c und konstruiere das ursprüngliche Dreieck und das Dreick, das diese Seitenmittelpunkte als Eckpunkte besitzt. Wie liegen die beiden Schwerpunkte zueinander?
Beachte: Werden Punkte und Vektoren addiert, so wird das Ergebnis stets als Punkt interpretiert.
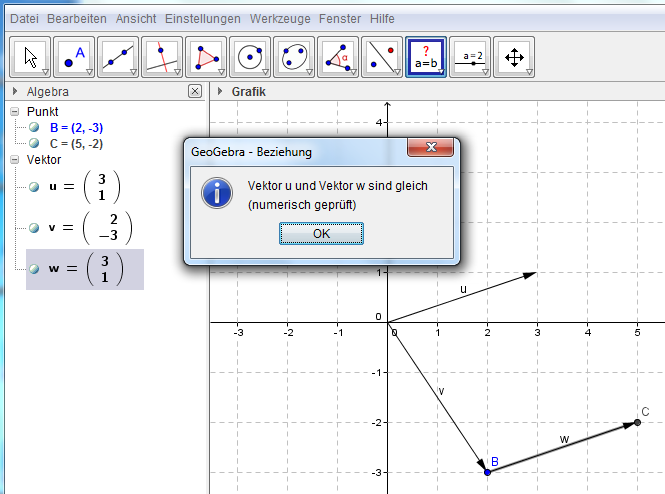
Ex: Ein Roboter bewegt sich vom Anfangspunkt A=(3|1) auf einem Polygonzug, der durch die folgenden Vektoren beschrieben wird: $\vec u$ = (4,2), $\vec v$ = (1,-5), $\vec w$ = (-6,3)
Stelle den Weg des Roboters graphisch dar und gib den Endpunkt seiner Bewegung an!
Beispiel: Vektoren festlegen, Punkte und Vektoren addieren, Beziehung zwischen Vektoren untersuchen
Beachte: Mit dem Werkzeug „Beziehung - Wähle zwei Objekte“ kann leicht überprüft werden, ob zwei Vektoren gleich sind.
Multiplikation mit Skalar
Abtragen von Strecken
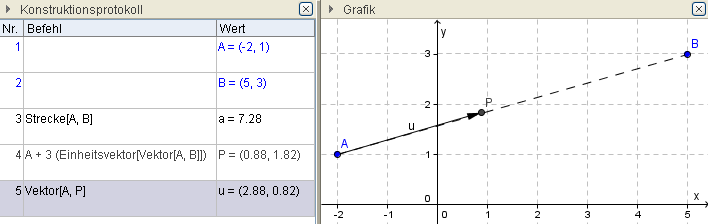
Ex: Trage vom Punkt A=(-2|1) eine Strecke mit der Länge 3E in Richtung des Punktes B=(5,3) ab!
Skalares Produkt
Ex: Zeige, dass das Skalarprodukt über die Beziehung $\vec a \cdot \vec b = |\vec a | \cdot |\vec b | \cdot \cos \varphi$ auch geometrisch gedeutet werden kann und berechne es für die beiden Vektoren $\vec a$ = (3,0) und $\vec b$ = (2,2) algebraisch und geometrisch.
Parallelität und Orthogonalität, Winkel zwischen Vektoren
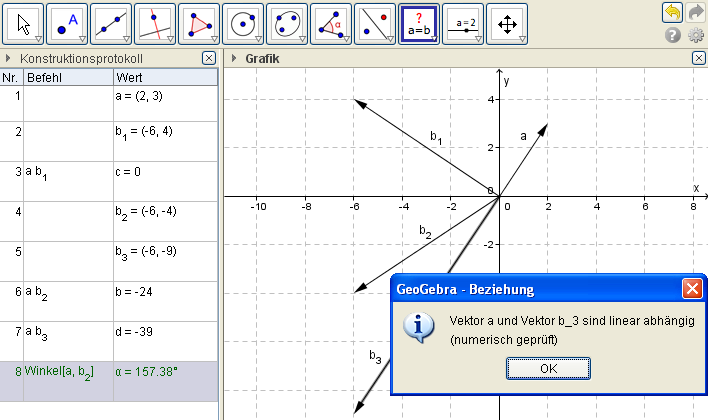
Ex: Überprüfe die folgenden Winkelpaare auf Parallelität bzw. Orthogonalität. Wenn keiner der beiden Fälle auftritt, berechne den Winkel zwischen ihnen.
a) $\vec a$ = (2,3), $\vec b_1$ = (-6,4)
b) $\vec a$ = (2,3), $\vec b_2$ = (-6,-4)
c) $\vec a$ = (2,3), $\vec b_3$ = (-6,-9)
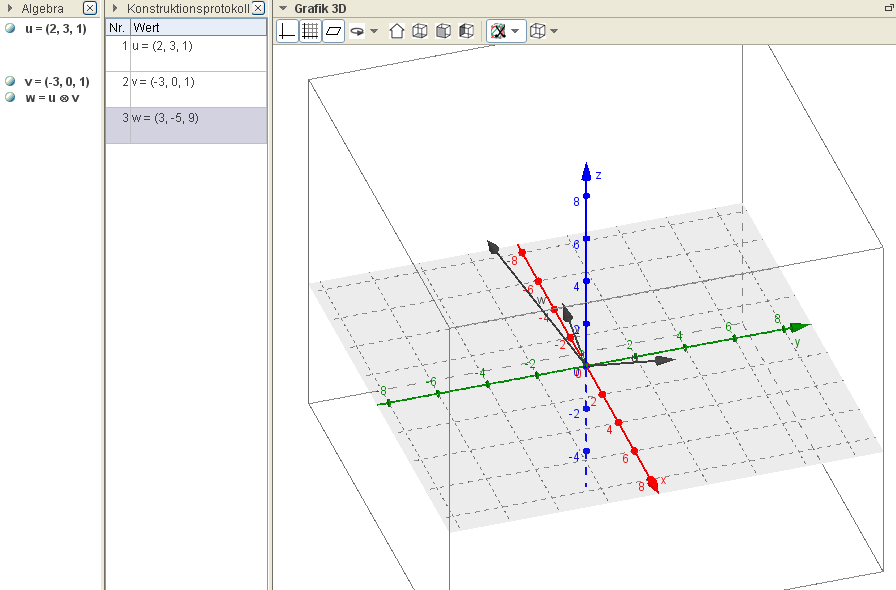
Vektorielles Produkt
Ex: Berechne das vektorielle Produkt der Vektoren $\vec u$ = (2,1,3) und $\vec v$ = (-3,0,1)
- Kreuzprodukt(<Vektor u>, <Vektor v>) liefert das Kreuzprodukt der beiden Vektoren (kann auch über den Operator ⊗ berechnet werden).