Folgen und Reihen
Ex: Ulam-Folge
a) Berechne für Startwerte $1\leq n \leq 20$ mit Hilfe der Tabellenkalkulation die Glieder der Ulam-Folge (bis Folgenglied 1 auftritt)
b) Stellle die Folgenglieder im $n-a_n-$Diagramm dar!
Hinweis: Beachte, dass der Vergleichsoperator in der Form == eingegeben werden muss (Wenn[Mod[B1, 2] ≟ 0, B1 / 2, 3B1 + 1])
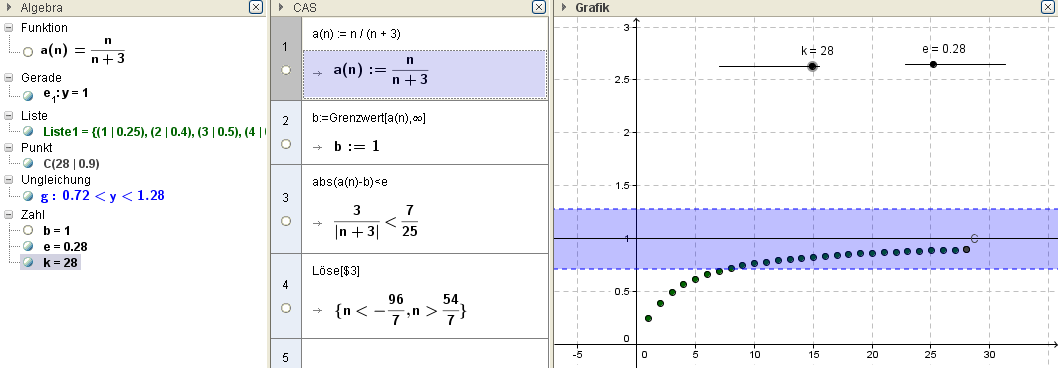
Ex: a) Berechne die ersten 30 Glieder der Folge `a(n)=3/(3+n)`
b) Gib eine graphische Darstellung der Folgenverlaufes an. (Verwende dazu den Befehl Folge[(i, a(i)), i, 1, k])
c) Berechne den Grenzwert der Folge `a(n)=3/(3+n)`
d) Veranschauliche die `\epsilon`-Umgebung für einige kleine Epsilons.
Ex: Iterationen
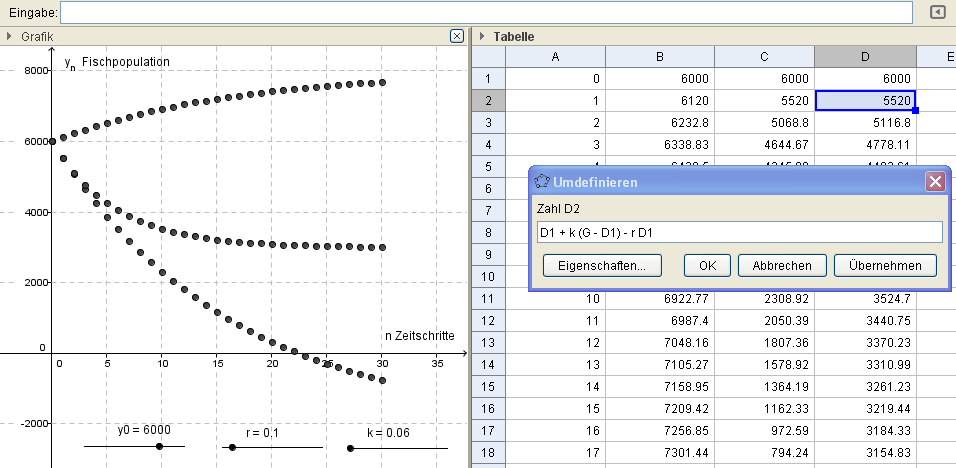
In einem See gibt es derzeit etwa 6000 Fische. Die maximal mögliche Fischmenge im See wird auf $G=8000$ geschätzt. Die Fischpopulation vermehre sich (im Wesentlichen nur) proportional zum aktuellen Freiraum mit einem Proportionalitätsfaktor von 6\%.
a) Entwickle ein mathematisches Modell zur Beschreibung des Fischbestandes im See in Form einer Differenzengleichung und führe mit einer Tabellenkalkulation eine Simulation durch.
b) Wie entwickelt sich der Fischbestand bei konstanter Fangrate, dh. wenn vereinbart wird, $10\%$ des Anfangsbestandes zu fangen? Stelle wieder eine Differenzengleichung auf und führe mit einer Tabellenkalkulation eine Simulation durch.
c) Wie entwickelt sich der Fischbestand bei variabler Fangrate, dh. wenn vereinbart wird, $10\%$ des jeweils aktuellen Bestandes zu fangen? Stelle wieder eine Differenzengleichung auf und führe mit einer Tabellenkalkulation eine Simulation durch.
d) Zeige, dass alle drei Differenzengleichungen vom Typ $y_{n+1} = a\cdot y_n + b $ sind.