Vorbemerkung: Die folgenden Ausführungen beziehen sich auf die aktuelle Betriebssystem-Version 3.10.
Aufgabe 56:
Findet heraus, wie ihr mit einem Computeralgebrasystem oder eurem Rechner
a) den Binomialkoeffizienten ![tex:{n \choose k}]() ,
,
b) ![tex:P (X = k)]() bei Binomialverteilung,
bei Binomialverteilung,
c) ![tex:P (a \leq X \leq b)]() bei Binomialverteilung
bei Binomialverteilung
berechnen könnt.
Ausführung:
a) nCr(n,k)
Beispiel: nCr(8,3)= 56
b) binompdf(n,p,k)
Beispiel: binompdf(8,0.5,3)= 0.21875
c) binomcdf(n,p,Untergrenze, Obergrenze)
Werden nur 3 Parameter verwendet, so wird der dritte Parameter als Obergrenze interpretiert, Untergrenze ist dann 0.
Beispiel: binompdf(8,0.5,0,3)= 0.363281
Achtung: Damit binompdf() und binomcdf() zur Verfügung steht, muss die Flash-Applikation TI-Stats/List Editor installiert sein.
Aufgabe 417:
Wie lassen sich mit einem CAS algebraische Gleichungen faktorisieren?
Ausführung:
Der Befehl factor() führt die Faktorisierung des angegebenen Polynoms über den reellen Zahlen aus.
Der Befehl cfactor() führt die Faktorisierung des angegebenen Polynoms über den komplexen Zahlen aus.
Aufgabe 428:
Wie lassen sich komplexe Zahlen mit einem Computeralgebra-System
a) von der Binomialform in die Polarform
b) von der Binomialform in die Exponentialform umwandeln ?
Ausführung:
Der Operator ▶Polar führt die gewünschte Umrechnung aus.
Das Ergebnis hängt von den entsprechenden Voreinstellungen.
a) Ist Gradmaß voreingestellt, so wird das Ergebnis in Polardarstellung angezeigt.
b) Ist Bogenmaß voreingestellt, so wird das Ergebnis im Exponentialdarstellung angezeigt.

Soll das Ergebnis numerisch ausgegeben werden, so muss im Modus Approximiert (Strg+Enter) vereinfacht werden.
Hinweis: die Umwandlung von der Polar- oder Exponentialdarstellung in die Binomaldarstellung lässt sich mit dem Operator ▶Rect bewerkstelligen.
Aufgabe 443:
Wie lassen sich mit einem Computeralgebra-System Potenzen komplexer Zahlen grafisch darstellen ?
Ausführung:
Aufgabe 454:
Wie lassen sich mit einem Computeralgebra-System Wurzeln komplexer Zahlen ermitteln ?
Ausführung:
Alle n-ten Wurzeln einer komplezen Zahl `z_0` erhält man indem man die entsprechende Gleichung
`z^n=z_0` lösen lässt. Dazu kann der Befehl cSolve(`z^n=z_0,z`) verwendet werden.
Beispiel: Ermittle die 3.Wurzeln aus -8.
cSolve(`z^3=-8,z`)
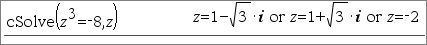
,
bei Binomialverteilung,
bei Binomialverteilung