Hinweis: Die Lösungen der folgenden Aufgaben beziehen sich auf die aktuelle Version 4.0 von Geogebra.
Aufgabe 56:
Findet heraus, wie ihr mit einem Computeralgebrasystem oder eurem Rechner
a) den Binomialkoeffizienten ![tex:{n \choose k}]() ,
,
b) ![tex:P (X = k)]() bei Binomialverteilung,
bei Binomialverteilung,
c) ![tex:P (a \leq X \leq b)]() bei Binomialverteilung
bei Binomialverteilung
berechnen könnt.
Ausführung:
a) BinomialKoeffizient[n,k]
Beispiel: BinomialKoeffizient[8,3]= 56
b) Binomial[n,p,k,false)
Beispiel: Binomial(8,0.5,3,false)= 0.21875
c) Binomial[n,p,k,false)
Beispiel: Binomial(8,0.5,3,true)= 0.363281
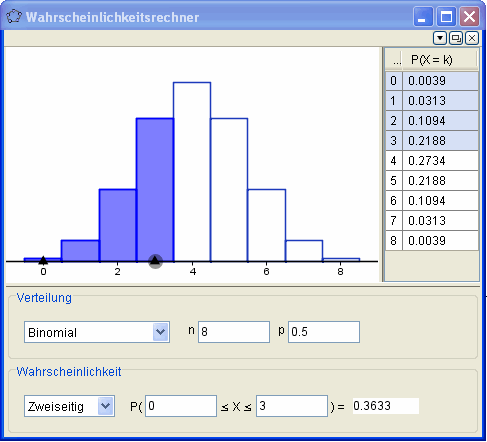
Hinweis: Mit den sogenannten Wahrscheinlichkeitsrechner (im Submenü des 3.letzten Icons von rechts zu finden) können Binomialverteilungen sehr schön (mit einer Visualisierung unterstützt) untersucht werden.
Aufgabe 417:
Wie lassen sich mit einem CAS algebraische Gleichungen faktorisieren?
Ausführung:
Der Befehl Factor() führt die Faktorisierung des angegebenen Polynoms über den reellen Zahlen aus.
Der Befehl CFactor() führt die Faktorisierung des angegebenen Polynoms über den komplexen Zahlen aus.

Aufgabe 428:
Wie lassen sich komplexe Zahlen mit einem Computeralgebra-System
a) von der Binomialform in die Polarform
b) von der Binomialform in die Exponentialform umwandeln ?
Ausführung:
a) Der Befehl ToPolar[] erledigt das Gewünschte.
b) Der Befehl ToExponential[] erledigt das Gewünschte.
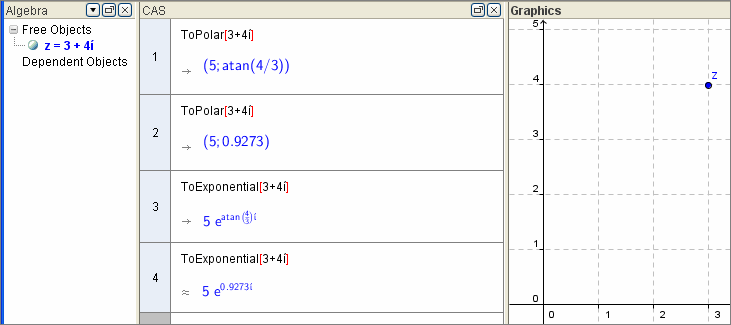
Das Ergebnis ist natürlich davon abhängig, ob exakt oder näherungsweise vereinfacht wird.
Aufgabe 443:
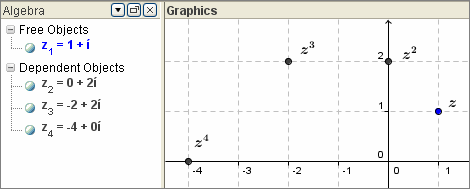
Wie lassen sich mit einem Computeralgebra-System Potenzen komplexer Zahlen grafisch darstellen ?
Ausführung:
Einzelne komplexe Zahlen werden automatisch geplottet, daher auch beliebige Potenzen.
Beispiel: Stelle die ersten vier Potenzen von 1+i grafisch dar.
Aufgabe 454:
Wie lassen sich mit einem Computeralgebra-System Wurzeln komplexer Zahlen ermitteln ?
Ausführung:
Alle n-ten Wurzeln einer komplezen Zahl `z_0` erhält man indem man die entsprechende Gleichung
`z^n=z_0` lösen lässt. Dazu kann in der CAS-Ansicht der Befehle CSolve oder CSolutions verwendet werden.
Beispiel: Ermittle die 3.Wurzeln aus -8.
CSolve[`z^3=-8`]

,
bei Binomialverteilung,
bei Binomialverteilung




