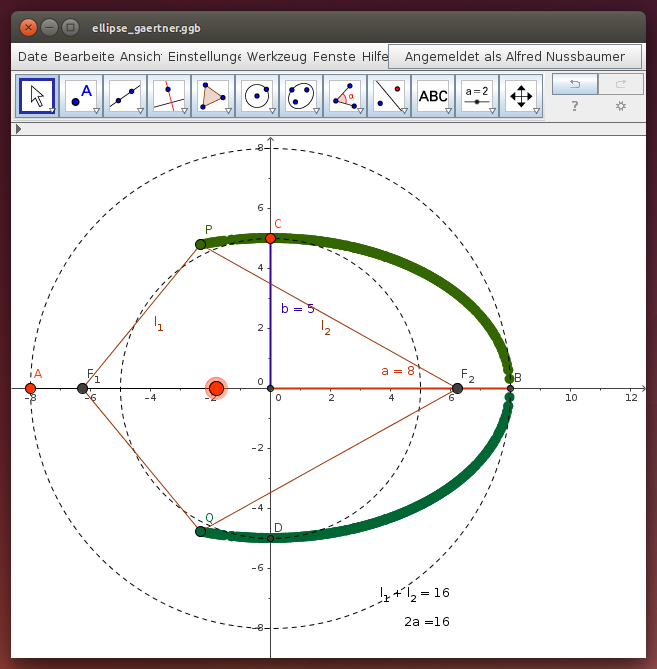
Konstruktion der Ellipse (Gärtnerkonstruktion)
Die Gärtnerkonstruktion fußt auf der Tatsache, dass die Summe der Abstände eines Punktes P der Ellipse zu den beiden Brennpunkten F1 und F2 konstant ist (): Fixiere die Endpunkte einer Schnur der Länge 2a an zwei Brennpunkten, spanne die Schnur mit einem Stab und fahre die Ellipse entlang der gespannten Schnur ab …
Wähle im folgenden GeoGebra-Applet die Länge der Hauptachse, indem du den Punkt A (Hauptscheitel) entlang der waagrechten Koordinatenachse verschiebst. Wähle die Lage der Brennpunkte, indem du den Punkt C (Nebenscheitel) entlang der senkrechten Koordinatenachse verschiebst. Beachte, dass du eine Ellipse in 1. Hauptlage (a > b) wählst!
Hinweis: Mit Strg-F kannst du die „Ansicht auffrischen“ - damit verschwinden schon bestehende Spuren.
Bewege dann den großen roten Punkt waagrecht zwischen den beiden Hauptscheiteln A und B und beobachte die Spur der beiden Punkte P und Q:
Aufgaben:
- Beobachte die Lage der beiden Brennpunkte: Sie liegen umso näher beisammen, je …
- Leite die Gleichung der Ellipse her!
zurück zu Ellipse | Kegelschnittslinien | Nichtlineare analytische Geometrie (R2)