Abkühlkurve
Heißer Tee kühlt in einer Tasse ab. Dabei sind folgende Temperaturwerte gegeben:
| Zeit (Minuten) | 0 | 2 | 5 | 10 | 15 | 30 | 45 | 60 |
| Temperatur (°C) | 68 | 65,2 | 61,3 | 55,5 | 50,5 | 39,5 | 32,4 | 28,0 |
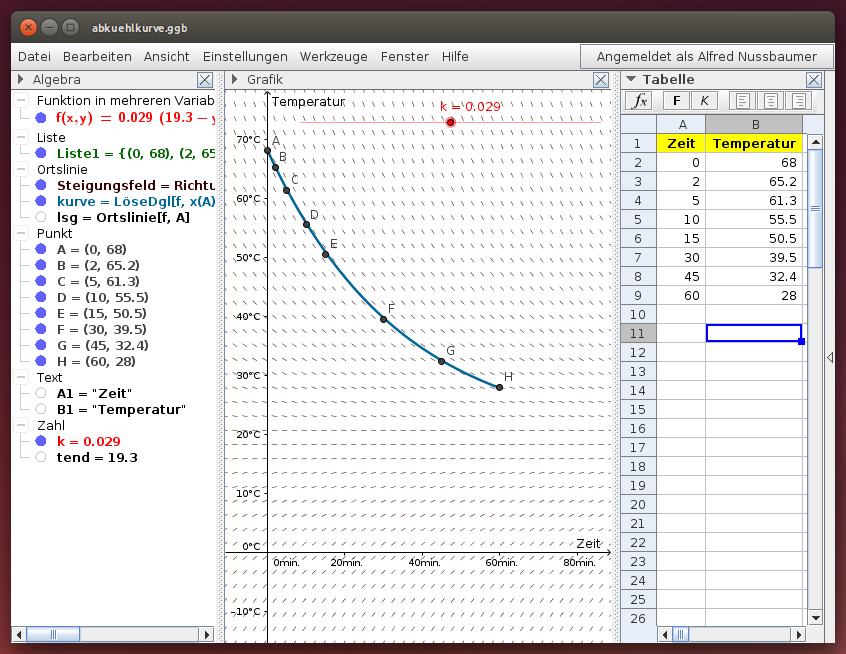
Visualisiere die Messwerte geeignet in einer Grafik und stelle die Differentialgleichung für die Abkühlkurve auf! Finde die Abkühlkurve, indem du sie durch den Anfangswert (0 | 68) legst und mit einem Schieberegler eine geeignete Konstante k bestimmst!
Lösung:
Aufgaben:
- Begründe, dass zur obigen Aufgabe die Differentialgleichung
passt (k = 0.029, G = 19.3)! Formuliere die Anfangsbedingung!
- Überprüfe, dass die Exponentialfunktion
genau die Lösung der obigen Differenzialgleichung ist!
- Im obigen Beispiel wurde die Endtemperatur tend mit einem Schieberegler auf 19,3 °C eingestellt. Beschreibe, wie sich die Abkühlkurve verändert, wenn die Endtemperatur niedriger ist!
Zurück zu Beschränktes Wachstumsmodell | Dynamische Systeme