Inhaltsverzeichnis
Funktionen - Festlegung
Termdefinierte Funktion
Ex: a) Erstelle den Graphen der Funktion $f(x)=5x^2$ (Fallweg nach x Sekunden Fallzeit)
b) Definiere einen Punkt P=(x0|f(x0)) am Graphen, wobei x0 über einen Schieberegler verändert werden soll
c) Trage Punkte, die P durchläuft in die Tabellenansicht ein.
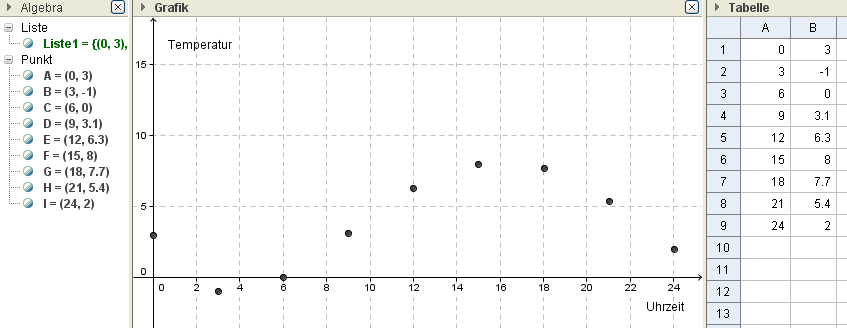
Empirische Funktionen
Funktion über Tabelle definiert
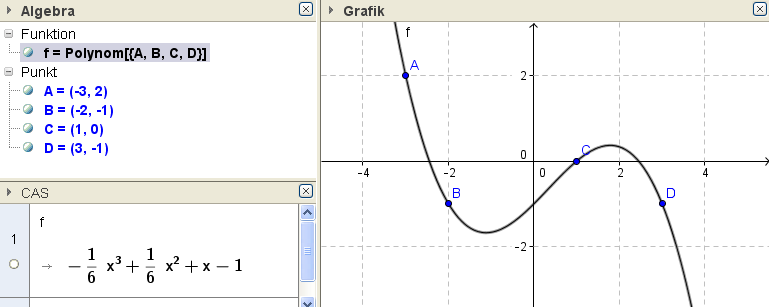
Polynom über Punkte definiert
Ex: Ermittle jenes Polynom, dessen Graph durch die Punkte A=(-3|2),B=(-2|-1),C=(1|0) und D=(3|-1) geht.
Hinweis: Verwende den Befehl Polynom(Liste von Punkten)
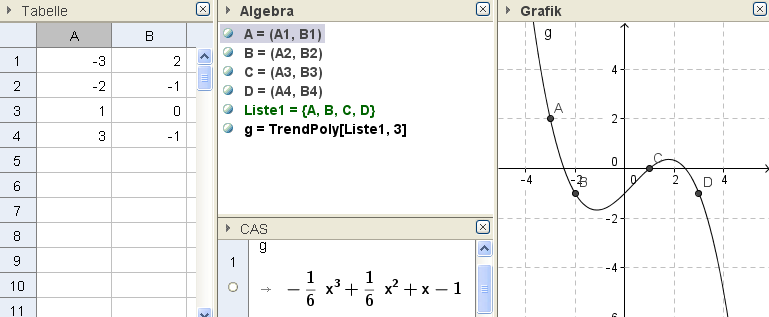
Funktion über Interpolation definiert
Ex: Ermittle jenes Polynom, dessen Graph durch die Punkte A=(-3|2),B=(-2|-1),C=(1|0) und D=(3|-1) geht.
Hinweis: Verwende den Befehl TrendPoly(Liste von Punkten,Grad)
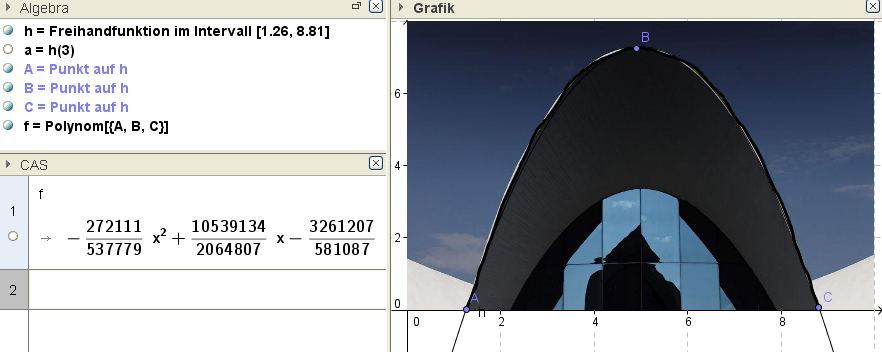
Über Graph definierte Funktion (Freihandfunktion)
Ex: Lade das Bild Oceanographic in das Graphikfenster und ermittle damit eine quadratische Funktion, die die am Bild dargestellte Parabel des Eingangsbereiches der Oceanographic-Unterwasser-Erlebniswelt in Valencia beschreibt.
Hinweis: Verwende das Werkzeug „Freihandskizze erkennen“ bzw. den Befehl Polynom(Liste von Punkten).
Funktion über Algorithmus definiert
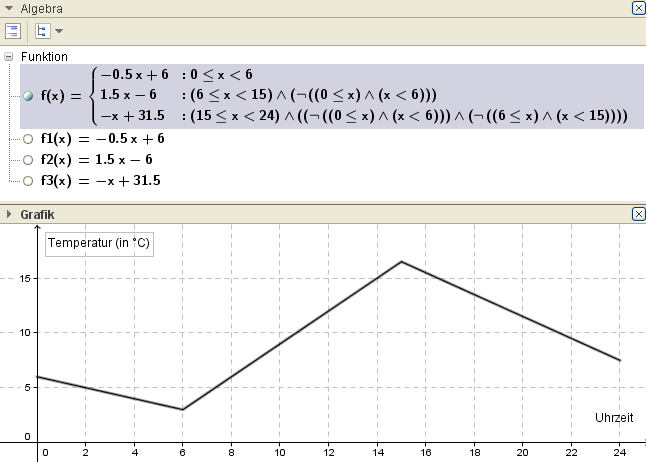
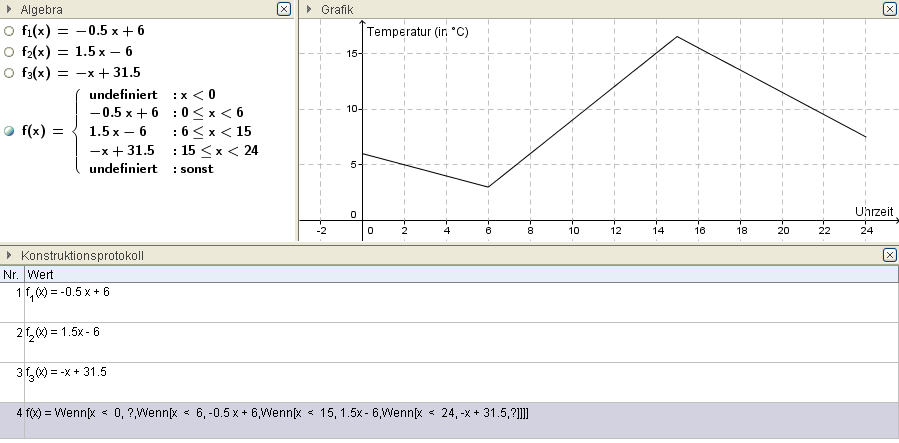
Abschnittsweise definierte Funktion
Funktionen mit Parametern
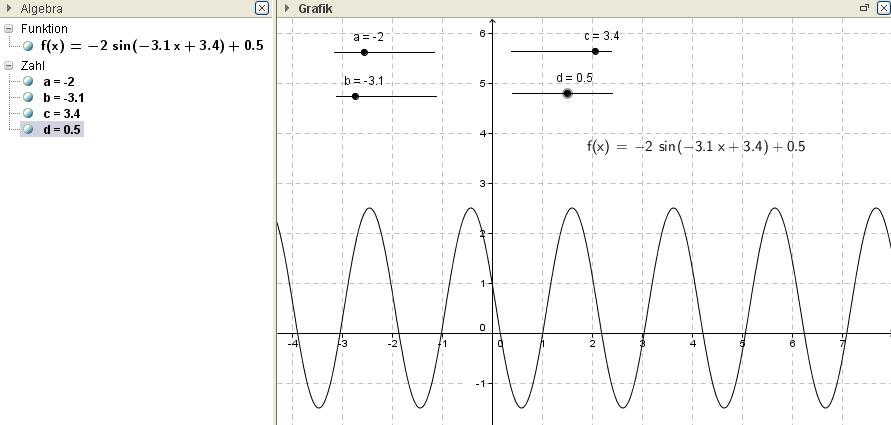
Ex: Führe an der allgemeinen Sinusfunktion f(x) = a * sin(b x + c) + d Parametervariation aus.
a) Welche Veränderungen am Graphen bewirken die einzelnen Parameter?
b) Weißt du welche physikalische Bedeutung sie besitzen?
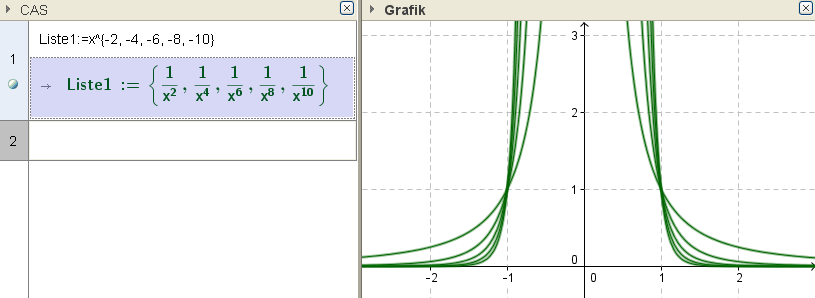
Scharen von Funktionsgraphen
Ex: Stelle die Potenzfunktionen $f_1(x)=x^{-2}, f_2(x)=x^{-4}, f_3(x)=x^{-6}, f_4(x)=x^{-8}, ...$ als Kurvenschar dar
Hinweis: Verwende dazu das CAS-Fenster.
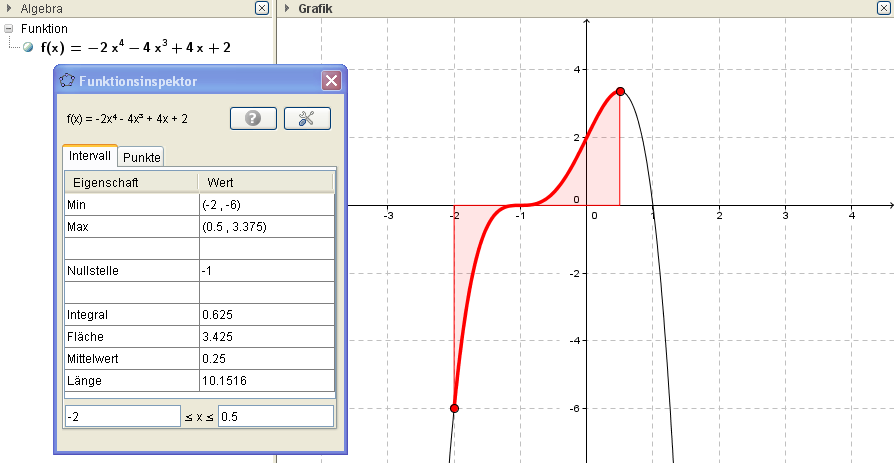
Funktionsinspektor
Ex: Gib die Nullstellen, Extremstellen und Wendepunkte der Funktion f(x)=-2x^4-4x^3+4x+2 an.
Nützliche Befehle:
- Funktion(Funktion,Startwert,Endwert) … Schränkt den Graphen der Funktion auf das angegebene Intervall ein. Hinweis:
Wenn(Intervall,Funktion)schränkt auch den Defintionsbereich der Funktion auf das Interfall ein. - Funktion(Liste) … Erzeugt aus der Liste eine abschnittsweise lineare Funktion (die erste beiden Werte der Liste geben den Definitionsbereich an).
- Schneide(Funktion1,Funktion2,Startwert,Endwert) … liefert die Schnittpunkte der beiden Funktionsgraphen im angegebeen Intervall (Startwert, Endwert kann auch entfallen).
- Nullstelle(Funktion,Startwert,Endwert) … Liefert die Nullpunkte der angegebenen Funktion. Wird nur der Startwert angegeben, wird das Newton-Verfahren zur Nullstellenbestimmung verwendet. Bei Polynomen braucht nur die Polynomfunktion angegeben werden.
- Nullstelle(Funktion,Startwert,Endwert) … Liefert die Nullpunkte der angegebenen Funktion.
- NullstellenListe(Liste) … erzeugt aus einer Liste der Nullstellen die entsprechenden Nullpunkte
- Extremum(Funktion,Startwert,Endwert) … Liefert die Extrema der betreffenden Funktion im angegebenen Intervall.
- Max(Funktion,Startwert,Endwert) … Liefert das Maximum der betreffenden Funktion im angegebenen Intervall. Dabei soll die Funktion nur ein Maximum in diesem Intervall haben.
- Min(Funktion,Startwert,Endwert) … Liefert die Minimum der betreffenden Funktion im angegebenen Intervall. Dabei soll die Funktion nur ein Minimum in diesem Intervall haben.
- Wendepunkt(Funktion) … liefert die Wendepunkte der betreffenden Funktion.
- Polynom(Liste von Punkten) … erzeugt ein Interpolationspolynom durch die angegebenen Punkte.
- Grad(Polynomfunktion) … liefert den Grad des angegebenen Polynoms
- Koeffizienten(Polynomfunktion) … liefert die Koeffizienten des angegebenen Polynoms (in Form einer Liste)
- Zähler(gebrochen rationale Funktion) … liefert den Zähler einer gebrochen rationalen Funktion
- Nenner(gebrochen rationale Funktion) … liefert den Nenner einer gebrochen rationalen Funktion
- Asymptote(Funktion) … liefert die Asymptoten der angegebenen Funktion (in Form einer Liste)
- Grenzwert(Funktion,Stelle) … liefert den Funktionsgrenzwert an der betreffenden Stelle
- LinksseitigerGrenzwert(Funktion,Stelle) … liefert den linksseitigen Funktionsgrenzwert an der betreffenden Stelle
- RechtsseitigerGrenzwert(Funktion,Stelle) … liefert den rechtsseitigen Funktionsgrenzwert an der betreffenden Stelle