Thema Pascal'sches Dreieck

(zu 5, S. 60 - 61)

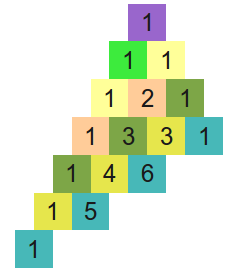
Wir haben gesehen, wie das Pascal'sche Dreieck aussieht:

                              1
                            1   1
                          1   2   1 
                        1   3   3   1 
                      1   4   6   4   1 
                    1   5  10   10  5   1

Schreibe dieses dreieckige Zahlenschema weiter auf. Ergänze mindestens 5 neue Zeilen!

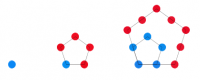
Dreieckszahlen

Wir zeichnen mit Hilfe von einzelnen Punkte immer größere Dreiecke. Das funktioniert so:

Zeichne weitere Dreiecke und zähle ab, wie viele Punkte du zum Zeichnen benötigst!

Wir erhalten die sogenannten Dreieckszahlen d_n:

→ d₁ = 1
→ d₂ = 1+2 = 3
→ d₃ = 3+3 = 6
→ d₄ = 6+4 = 10
→ d₅ = 10+5 = 15

Setze die Liste der Dreieckszahlen fort.
Die Dreieckszahlen kommen auch im Pascal'schen Dreieck vor! Suche sie!
Berechne die Summe von je zwei benachbarten Dreieckszahlen. Was fällt dir auf? Kannst du deine Vermutung beweisen?
Berechne die Differenz von je zwei benachbarten Dreieckszahlen. Was fällt dir auf? Kannst du deine Vermutung beweisen?
Begründe, warum gilt: d_n = 1 + 2 + 3 + … + n
Zeige folgende Formel: $tex:d_n=\frac{n(n+1)}{2}$

Die Dreieckszahlen besitzen eine bemerkenswerte Eigenschaft: Jede natürliche Zahl lässt sich als Summe von höchstens 3 Dreieckszahlen schreiben.

Beispiel: 67 = 36 + 21 + 10

Überlege, wie die Zahlen 48, 62, 85 und 91 als Summe von maximal 3 Dreieckszahlen gebildet werden können.
Schreibe weitere natürliche Zahlen als Summe von maximal 3 Dreieckszahlen!

Quadratzahlen

Ähnlich wie bei den Dreieckszahlen zeichnen wir mit Hilfe einzelner Punkte immer größere Quadrate:

Zeichne weitere Dreiecke und zähle ab, wie viele Punkte du zum Zeichnen benötigst!

Wir erhalten die Quadratzahlen d_n:

→ q₁ = 1
→ q₂ = 1+3 = 4
→ q₃ = 4+5 = 9
→ q₄ = 9+7 = 16

Setze die Liste der Quadratzahlen fort.
Begründe, warum gilt: d_n = 1 + 3 + 5 + … + (2n-1)
Zeige folgende Formel:
Jede Quadratzahl ist die Summe von zwei Dreieckszahlen! Veranschauliche diese Aussage durch eine graphische Darstellung! Versuche, diese Aussage präzise zu formulieren und rechnerisch zu beweisen!
Die Summe der ersten n Quadratzahlen nennt man Pyramidenzahl: $tex:p_n=1^2+2^2+3^2+\ldots+n^2$ . Berechne die ersten 5 Pyramidenzahlen.
Überprüfe die Formel $tex:p_n=\frac{n(n+1)(2n+1)}{6}$

Finde die Liste der Fünfeckszahlen. Verwende dazu folgende Grafik:
Versuche, für die Fünfeckzahlen ähnliche Eigenschaften zu finden, wie sie für Dreick- und Quadratzahlen gültig sind.

Fibonacci Zahlen

Die Folge der Fibonacci-Zahlen wurde um 1200 von Leonardo Fibonacci (ca. 1180 - 1240, Pisa) benutzt, um die Zunahme einer Kaninchenpopulation zu beschreiben.

Am Beginn gibt es ein Paar Kaninchen, die geschlechtsreif sind.
Jedes geschlechtsreife Paar bringt pro Monat ein Paar Kaninchen zur Welt.
Ein neugeborenes Paar wird im zweiten Monat geschlechtsreif.

Damit erhalten wir:

Monat: 1 Pärchen (nicht geschlechtsreif)
Monat: 1 Pärchen (geschlechtsreif)
Monat: 2 Pärchen (1 geschlechtsreif; 1 nicht geschlechtsreif)
Monat: 3 Pärchen (2 geschlechtsreif; 1 nicht geschlechtsreif)
Monat: 5 Pärchen (3 geschlechtsreif; 2 nicht geschlechtsreif)
Monat: 8 Pärchen (5 geschlechtsreif; 3 nicht geschlechtsreif)

usw.

Wir erhalten die Fibonaccizahlen f_n:

→ f₁ = 1
→ f₂ = 1
→ f₃ = 1+1 = 2
→ f₄ = 1+2 = 3
→ f₅ = 2+3 = 5
→ f₆ = 3+5 = 8

Setze die Liste der Fibonaccizahlen fort.
Überlege, dass gilt: Die Summe der Quadrate zweier benachbarter Fibonaccizahlen ist wieder eine Fibonaccizahl.
Überlege, dass gilt: und und usw.
Die Fibonaccizahlen kommen ebenfalls im Pascal'schen Dreieck vor. Folgende Abbildung zeigt einen Ausschnitt aus dem Pascal'schen Dreieck und soll dir helfen, sie in diesem Dreieck zu finden:

Hinweis: Betrachte Kästchen mit gleicher Farbe gemeinsam!

Weblinks:

Fibonacci-Zahlen (Mathematik zum Anfassen BRα) - MediaPlayer erforderlich
Figurierte Zahlen (MathSpace, Prof. Dr. Rudolf Taschner) - MediaPlayer erforderlich
Binomialkoeffizienten (MathSpace, Prof. Dr. Rudolf Taschner) - MediaPlayer erforderlich
Blaise Pascal (MathSpace, Prof. Dr. Rudolf Taschner) - MediaPlayer erforderlich

Ausblick

Kombinatorik (siehe Thema Mathematik 6)
Binomischer Lehrsatz (siehe Thema Mathematik 7)