| Zurück zu: 5.Klasse » Analytische Geometrie der Ebene | Technologie-Tipps zur Normalvektorform der Geradengleichung in der Ebene |
Normalvektorform der Geradengleichung in der Ebene
(zu  5, S. 212 - 213, zu BIFIE GK AG3.5)
5, S. 212 - 213, zu BIFIE GK AG3.5)
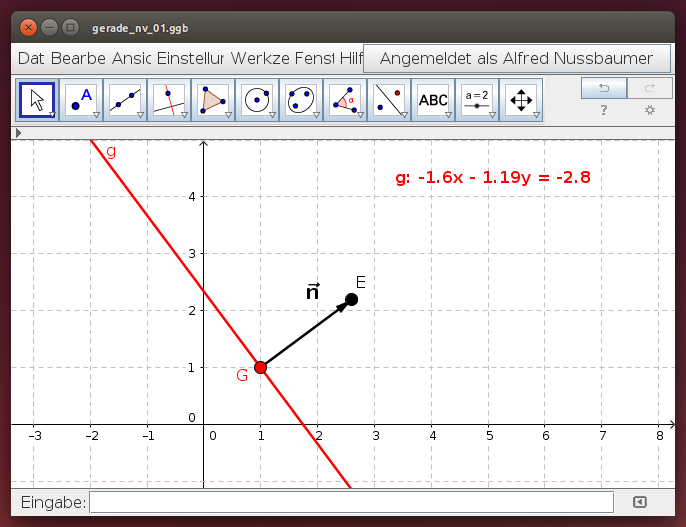
Ein Punkt G und der Normalvektor legen in der Ebene die Gerade g eindeutig fest. Ziehe im folgenden Beispiel den Punkt G an die gewünschte Stelle, drehe den Normalvektor mit dem Punkt E in die gewünschte Richtung und vergleiche die Geradengleichung für g mit der Lage der Geraden!
Aufgaben:
- Lege eine Gerade parallel zu den Koordinatenachsen und lies ihre Gleichung ab!
- Verschiebe den Punkt G vertikal (parallel zur y-Achse) und interpretiere die Änderung der Geradengleichung!
- Verschiebe den Punkt G horizontal (parallel zur x-Achse). Kannst du auch diesmal eine Gesetzmäßigkeit entdecken (Hinweis: verschiebe den Punkt G um gleiche Strecken und beobachte den Zuwachs oder die Abnahme der Konstanten in der Geradengleichung für g)!
Zurück zu Analytische Geometrie der Ebene