Inhaltsverzeichnis
Die Folge der Obersummen und Untersummen ...
Wir betrachten eine auf dem Intervall [a; b] positive Funktion f und berechnen den Flächeninhalt unter dem Graphen von f näherungsweise mit Hilfe von Ober- und Untersummen. Konvergieren die Folgen der Obersummen und Untersummen zum selben Grenzwert, so ist dies der Flächeninhalt unter dem Graphen.
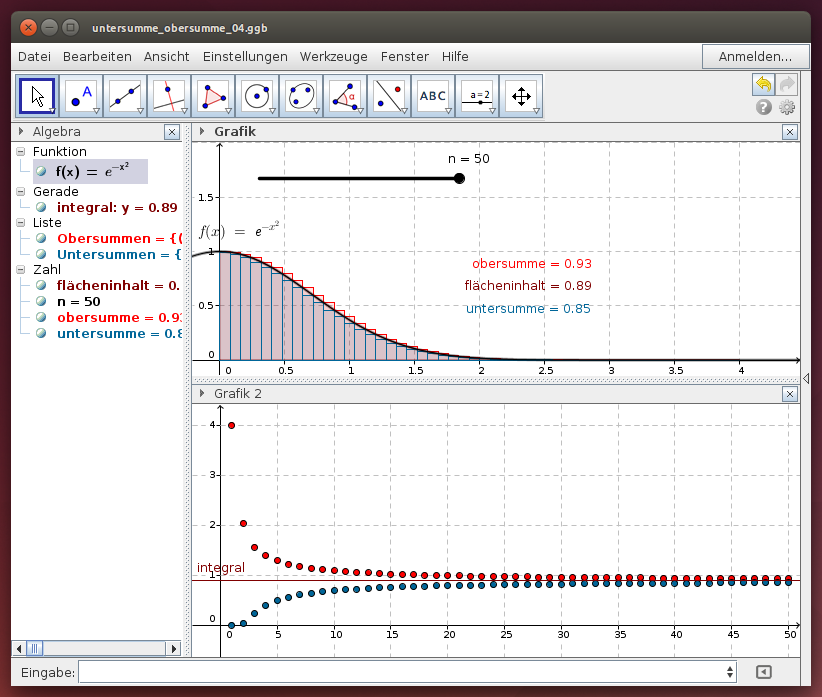
Beispiel: Die Exponentialfunktion f(x) = exp(-x^2)
Wir berechnen den Flächeninhalt unter dem Funktionsgraphen über dem Intervall [0; 4] näherungsweise mit Rechteckstreifen und bilden für n Streifen jeweils die Obersumme und die Untersumme:
Aufgaben:
- Begründe, dass die Obersumme stets größer als der Flächeninhalt unter dem Graphen ist!
- Begründe, dass die Untersumme stets kleiner als der Flächeninhalt unter dem Graphen ist!
- Wähle verschiedene Werte für die Anzahl n der Rechteckstreifen und beobachte, ob die Ober- und Untersumme zum gleichen Grenzwert konvergieren (könnten)!
- Wähle andere Funktionen, die im Intervall [0; 4] positiv sind und beobachte das Verhalten der Folgen der Ober- und Untersumme!
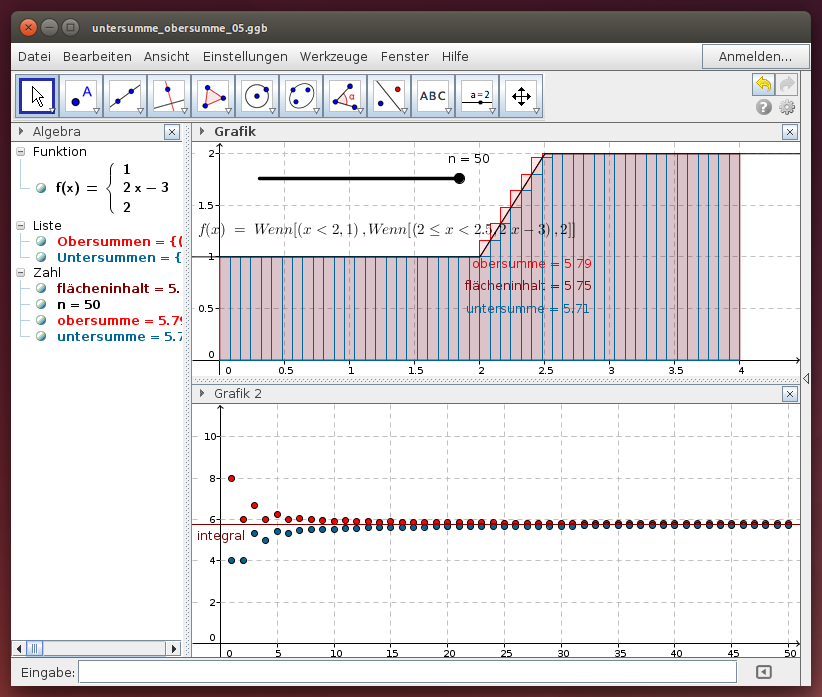
Zur Monotonie der Folgen der Obersummen und Untersummen
Muss die Folge der Obersummen zu einer über einem Intervall [a; b] positiven Funktion monoton fallen?
Beantworte die analoge Frage zur Monotonie der Folge von Untersummen!
Hinweis:
Ob die Folge der Obersummen (und die Folge der Untersummen) monoton ist oder nicht, spielt für die Definition des Flächeninhalts keine Rolle. Entscheidend ist, dass beide Folgen zum selben Grenzwert konvergieren …
Zurück zu Grundlagen der Integralrechnung